Cây bao trùm là một đồ thị con được liên kết và vô hướng nối tất cả các đỉnh. Nhiều cây bao trùm có thể tồn tại trong một biểu đồ. Cây bao trùm tối thiểu (MST) trên mỗi đồ thị có cùng trọng số hoặc nhỏ hơn tất cả các cây bao trùm khác. Trọng số được gán cho các cạnh của cây bao trùm và tổng là trọng số được gán cho mỗi cạnh. Vì V là số đỉnh trong đồ thị nên cây khung tối thiểu có các cạnh là (V - 1), trong đó V là số cạnh.
Tìm cây bao trùm tối thiểu bằng thuật toán của Kruskal
-
Tất cả các cạnh phải được sắp xếp theo thứ tự trọng lượng không giảm dần.
-
Chọn cạnh nhỏ nhất. Cạnh này được bao gồm nếu chu trình không được hình thành.
-
Bước 2 sẽ được thực hiện cho đến khi cây khung có các cạnh (V-1).
Trong trường hợp này, chúng tôi được yêu cầu sử dụng một phương pháp tham lam. Tùy chọn tham lam là chọn cạnh có khối lượng ít nhất. Như một minh họa:Cây bao trùm tối thiểu cho biểu đồ này là (9-1) =8 cạnh.
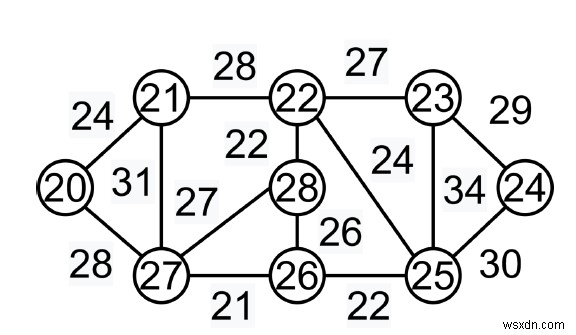
After sorting: Weight Src Dest 21 27 26 22 28 22 22 26 25 24 20 21 24 22 25 26 28 26 27 22 23 27 27 28 28 20 27 28 21 22 29 23 24 30 25 24 31 21 27 34 23 25
Bây giờ chúng ta cần chọn tất cả các cạnh theo cách sắp xếp.
Cạnh 26-27-> được bao gồm vì không có chu trình nào được hình thành
Cạnh 28-22-> được bao gồm vì không có chu trình nào được hình thành
Cạnh 26-25-> được bao gồm vì không có chu trình nào được hình thành.
Cạnh 20-21-> được bao gồm vì không có chu trình nào được hình thành
Cạnh 22-25-> được bao gồm vì không có chu trình nào được hình thành.
Cạnh 28-26-> bị loại bỏ khi chu kỳ được hình thành
Cạnh 22-23-> được bao gồm vì không có chu trình nào được hình thành
Cạnh 27-28-> bị loại bỏ khi chu kỳ được hình thành
Cạnh 20-27-> được bao gồm vì không có chu trình nào được hình thành
Cạnh 21-22-> bị loại bỏ khi chu kỳ được hình thành
Cạnh 23-24-> được bao gồm vì không có chu trình nào được hình thành
Vì số cạnh là (V-1), vì vậy thuật toán kết thúc ở đây.
Ví dụ
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E){
struct Graph* graph = (struct Graph*)(malloc(sizeof(struct Graph)));
graph->V = V;
graph->E = E;
graph->edge = (struct Edge*)malloc(sizeof( struct Edge)*E);
return graph;
}
struct subset {
int parent;
int rank;
};
int find(struct subset subsets[], int i){
if (subsets[i].parent != i)
subsets[i].parent
= find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(struct subset subsets[], int x, int y){
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
int myComp(const void* a, const void* b){
struct Edge* a1 = (struct Edge*)a;
struct Edge* b1 = (struct Edge*)b;
return a1->weight > b1->weight;
}
void KruskalMST(struct Graph* graph){
int V = graph->V;
struct Edge
result[V];
int e = 0;
int i = 0;
qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);
struct subset* subsets
= (struct subset*)malloc(V * sizeof(struct subset));
for (int v = 0; v < V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
while (e < V - 1 && i < graph->E) {
struct Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
}
printf("Following are the edges in the constructed MST\n");
int minimumCost = 0;
for (i = 0; i < e; ++i){
printf("%d -- %d == %d\n", result[i].src,
result[i].dest, result[i].weight);
minimumCost += result[i].weight;
}
printf("Minimum Cost Spanning tree : %d",minimumCost);
return;
}
int main(){
/* Let us create the following weighted graph
30
0--------1
| \ |
26| 25\ |15
| \ |
22--------23
24 */
int V = 24;
int E = 25;
struct Graph* graph = createGraph(V, E);
graph->edge[0].src = 20;
graph->edge[0].dest = 21;
graph->edge[0].weight = 30;
graph->edge[1].src = 20;
graph->edge[1].dest = 22;
graph->edge[1].weight = 26;
graph->edge[2].src = 20;
graph->edge[2].dest = 23;
graph->edge[2].weight = 25;
graph->edge[3].src = 21;
graph->edge[3].dest = 23;
graph->edge[3].weight = 35;
graph->edge[4].src = 22;
graph->edge[4].dest = 23;
graph->edge[4].weight = 24;
KruskalMST(graph);
return 0;
} Đầu ra
Following are the edges in the constructed MST 22 -- 23 == 24 20 -- 23 == 25 20 -- 21 == 30 Minimum Cost Spanning tree : 79
Kết luận
Hướng dẫn này đã trình bày cách sử dụng phương pháp Thuật toán-Greedy của cây kéo dài tối thiểu của Kruskal và mã C ++ để giải quyết vấn đề này. Chúng tôi cũng có thể viết mã này bằng java, python và các ngôn ngữ khác. Nó được mô phỏng theo ý tưởng của Kruskal. Chương trình này tìm cây khung ngắn nhất trong một đồ thị nhất định. Chúng tôi hy vọng bạn thấy hướng dẫn này hữu ích.
