Có một đồ thị liên thông G (V, E) và trọng số hoặc chi phí cho mọi cạnh đã cho. Thuật toán của Kruskal sẽ tìm cây bao trùm tối thiểu bằng cách sử dụng biểu đồ và chi phí.
Đó là cách tiếp cận cây hợp nhất. Ban đầu có các cây khác nhau, thuật toán này sẽ hợp nhất chúng bằng cách lấy các cạnh có chi phí nhỏ nhất và tạo thành một cây duy nhất.
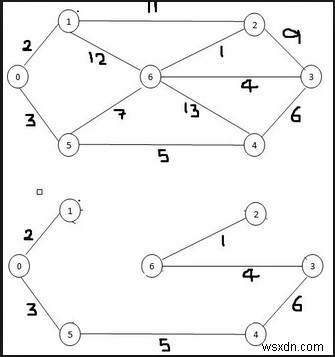
Trong bài toán này, tất cả các cạnh được liệt kê và sắp xếp dựa trên chi phí của chúng. Từ danh sách, các cạnh có chi phí tối thiểu được lấy ra và thêm vào cây, và mọi thứ sẽ được kiểm tra xem chu trình hình thành cạnh hay không, nếu nó tạo thành một chu trình thì loại bỏ cạnh đó khỏi danh sách và chuyển sang cạnh tiếp theo.
-
Độ phức tạp thời gian của thuật toán này là O (E log E) hoặc O (E log V), trong đó E là số cạnh và V là số đỉnh.
Đầu vào - Ma trận kề
0 1 3 4 ∞ 5 ∞ 1 0 ∞ 7 2 ∞ ∞ 3 ∞ 0 ∞ 8 ∞ ∞ 4 7 ∞ 0 ∞ ∞ ∞ ∞ 2 8 ∞ 0 2 4 5 ∞ ∞ ∞ 2 0 3 ∞ ∞ ∞ ∞ 4 3 0
Đầu ra -
Edge: B--A And Cost: 1 Edge: E--B And Cost: 2 Edge: F--E And Cost: 2 Edge: C--A And Cost: 3 Edge: G--F And Cost: 3 Edge: D--A And Cost: 4 Total Cost: 15
Thuật toán
kruskal (g:Graph, t:Tree)
Đầu vào - Đồ thị g đã cho và một cây rỗng t
Đầu ra - Cây có các cạnh đã chọn
Begin create set for each vertices in graph g for each set of vertex u do add u in the vertexSet[u] done sort the edge list. count := 0 while count <= V – 1 do //as tree must have V – 1 edges ed := edgeList[count] //take an edge from edge list if the starting vertex and ending vertex of ed are in same set then merge vertexSet[start] and vertexSet[end] add the ed into tree t count := count + 1 done End
Ví dụ
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 1, 3, 4, INF, 5, INF},
{1, 0, INF, 7, 2, INF, INF},
{3, INF, 0, INF, 8, INF, INF},
{4, 7, INF, 0, INF, INF, INF},
{INF, 2, 8, INF, 0, 2, 4},
{5, INF, INF, INF, 2, 0, 3},
{INF, INF, INF, INF, 4, 3, 0}
};
typedef struct{
int u, v, cost;
}edge;
void swapping(edge &e1, edge &e2){
edge temp;
temp = e1;
e1 = e2;
e2 = temp;
}
class Tree{
int n;
edge edges[V-1]; //as a tree has vertex-1 edges
public:
Tree(){
n = 0;
}
void addEdge(edge e){
edges[n] = e; //add edge e into the tree
n++;
}
void printEdges(){ //print edge, cost and total cost
int tCost = 0;
for(int i = 0; i<n; i++){
cout << "Edge: " << char(edges[i].u+'A') << "--" << char(edges[i].v+'A');
cout << " And Cost: " << edges[i].cost << endl;
tCost += edges[i].cost;
}
cout << "Total Cost: " << tCost << endl;
}
};
class VSet{
int n;
int set[V];//a set can hold maximum V vertices
public:
VSet(){
n = -1;
}
void addVertex(int vert){
set[++n] = vert; //add vertex to the set
}
int deleteVertex(){
return set[n--];
}
friend int findVertex(VSet *vertSetArr, int vert);
friend void merge(VSet &set1, VSet &set2);
};
void merge(VSet &set1, VSet &set2){
//merge two vertex sets together
while(set2.n >= 0)
set1.addVertex(set2.deleteVertex());
//addToSet(vSet1, delFromSet(vSet2));
}
int findVertex(VSet *vertSetArr, int vert){
//find the vertex in different vertex sets
for(int i = 0; i<V; i++)
for(int j = 0; j<=vertSetArr[i].n; j++)
if(vert == vertSetArr[i].set[j])
return i;//node found in i-th vertex set
}
int findEdge(edge *edgeList){
//find the edges from the cost matrix of Graph and store to edgeList
int count = -1, i, j;
for(i = 0; i<V; i++)
for(j = 0; j<i; j++)
if(costMat[i][j] != INF){
count++;
//fill edge list for the position 'count'
edgeList[count].u = i; edgeList[count].v = j;
edgeList[count].cost = costMat[i][j];
}
return count+1;
}
void sortEdge(edge *edgeList, int n){
//sort the edges of graph in ascending order of cost
int flag = 1, i, j;
for(i = 0; i<(n-1) && flag; i++){//modified bubble sort is used
flag = 0;
for(j = 0; j<(n-i-1); j++)
if(edgeList[j].cost > edgeList[j+1].cost){
swapping(edgeList[j], edgeList[j+1]);
flag = 1;
}
}
}
void kruskal(Tree &tr){
int ecount, maxEdge = V*(V-1)/2; //max n(n-1)/2 edges can have in a graph
edge edgeList[maxEdge], ed;
int uloc, vloc;
VSet VSetArray[V];
ecount = findEdge(edgeList);
for(int i = 0; i < V; i++)
VSetArray[i].addVertex(i);//each set contains one element
sortEdge(edgeList, ecount); //ecount number of edges in the graph
int count = 0;
while(count <= V-1){
ed = edgeList[count];
uloc = findVertex(VSetArray, ed.u);
vloc = findVertex(VSetArray, ed.v);
if(uloc != vloc){ //check whether source abd dest is in same set or not
merge(VSetArray[uloc], VSetArray[vloc]);
tr.addEdge(ed);
}
count++;
}
}
int main(){
Tree tr;
kruskal(tr);
tr.printEdges();
} Đầu ra
Edge: B--A And Cost: 1 Edge: E--B And Cost: 2 Edge: F--E And Cost: 2 Edge: C--A And Cost: 3 Edge: G--F And Cost: 3 Edge: D--A And Cost: 4 Total Cost: 15
