Thuật toán MST của Prim (Cây kéo dài tối thiểu)

Có một đồ thị liên thông G (V, E) và trọng số hoặc chi phí cho mọi cạnh đã cho. Thuật toán của Prim sẽ tìm cây bao trùm nhỏ nhất từ ​​biểu đồ G.

Đó là cách tiếp cận cây đang phát triển. Thuật toán này cần một giá trị hạt giống để bắt đầu cây. Đỉnh hạt được phát triển để tạo thành toàn bộ cây.

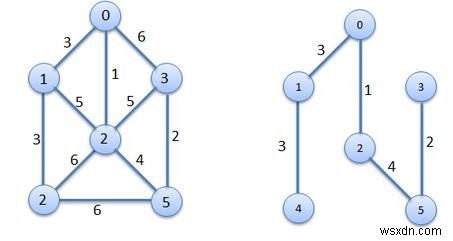
Vấn đề sẽ được giải quyết bằng cách sử dụng hai bộ. Một tập hợp chứa các nút đã được chọn và một tập hợp khác giữ mục chưa được xem xét. Từ đỉnh hạt giống, nó lấy các đỉnh liền kề, dựa trên chi phí cạnh tối thiểu, do đó nó phát triển cây bằng cách lấy từng nút một.

• Độ phức tạp thời gian của bài toán này là O (V2). Ở đây V là số đỉnh.

Đầu vào - Danh sách gần kề -

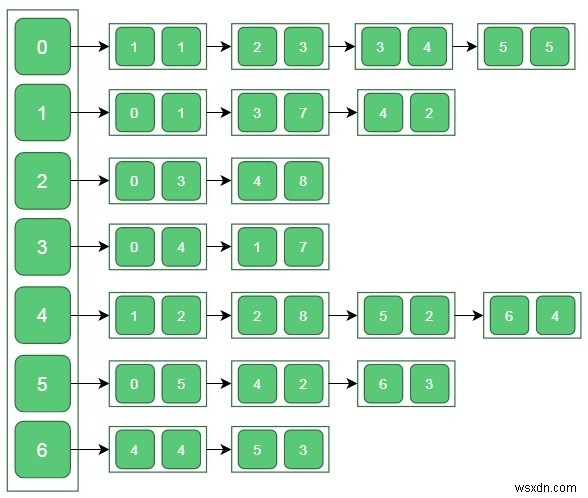
Đầu ra -

(0)---(1|1) (0)---(2|3) (0)---(3|4)
(1)---(0|1) (1)---(4|2)
(2)---(0|3)
(3)---(0|4)
(4)---(1|2) (4)---(5|2)
(5)---(4|2) (5)---(6|3)
(6)---(5|3)

Thuật toán

prims (g:Graph, t:tree, start)

Đầu vào - Biểu đồ g, Một cây trống và đỉnh hạt có tên là ‘start’ Đầu ra:Cây sau khi thêm các cạnh.

Begin
   define two sets as usedVert, unusedVert
   usedVert[0] := start and unusedVert[0] := φ
   for all vertices except start do
      usedVert[i] := φ
      unusedVert[i] := i //add all vertices in unused list
   done
   while number of vertices in usedVert ≠ V do //V is number of total nodes
      min := ∞
      for all vertices of usedVert array do
         for all vertices of the graph do
            if min > cost[i,j] AND i ≠ j then
               min := cost[i,j]
               ed := edge between i and j, and cost of ed := min
            done
         done
         unusedVert[destination of ed] := φ
         add edge ed into the tree t
         add source of ed into usedVert
   done
End

Ví dụ (C ++)

#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
   {0, 1, 3, 4, INF, 5, INF},
   {1, 0, INF, 7, 2, INF, INF},
   {3, INF, 0, INF, 8, INF, INF},
   {4, 7, INF, 0, INF, INF, INF},
   {INF, 2, 8, INF, 0, 2, 4},
   {5, INF, INF, INF, 2, 0, 3},
   {INF, INF, INF, INF, 4, 3, 0}
};
typedef struct{
   int u, v, cost;
}edge;
class Tree{
   int n;
   edge edges[V-1]; //as a tree has vertex-1 edges
   public:
   Tree(){
      n = 0;
   }
   void addEdge(edge e){
      edges[n] = e; //add edge e into the tree
      n++;
   }
   void printEdges(){ //print edge, cost and total cost
      int tCost = 0;
      for(int i = 0; i<n; i++){
         cout << "Edge: " << char(edges[i].u+'A') < "--" << char(edges[i].v+'A');
         cout << " And Cost: " << edges[i].cost << endl;
         tCost += edges[i].cost;
      }
      cout << "Total Cost: " << tCost << endl;
   }
   friend void prims(Tree &tre, int start);
};
void prims(Tree &tr, int start){
   int usedVert[V], unusedVert[V];
   int i, j, min, p;
   edge ed;
   //initialize
   usedVert[0] = start; p = 1;
   unusedVert[0] = -1;//-1 indicates the place is empty
   for(i = 1; i<V; i++){
      usedVert[i] = -1;//all places except first is empty
      unusedVert[i] = i;//fill with vertices
   }
   tr.n = 0;
   //get edges and add to tree
   while(p != V){ //p is number of vertices in usedVert array
      min = INF;
      for(i = 0; i<p; i++){
         for(j = 0; j<V; j++){
            if(unusedVert[j] != -1){
               if(min > costMat[i][j] && costMat[i][j] != 0){
                  //find the edge with minimum cost
                  //such that u is considered and v is not considered yet
                  min = costMat[i][j];
                  ed.u = i; ed.v = j; ed.cost = min;
               }
            }
         }
      }
      unusedVert[ed.v] = -1;//delete v from unusedVertex
      tr.addEdge(ed);
      usedVert[p] = ed.u; p++;//add u to usedVertex
   }
}
main(){
   Tree tr;
   prims(tr, 0); //starting node 0
   tr.printEdges();
}

Đầu ra

(0)---(1|1) (0)---(2|3) (0)---(3|4)
(1)---(0|1) (1)---(4|2)
(2)---(0|3)
(3)---(0|4)
(4)---(1|2) (4)---(5|2)
(5)---(4|2) (5)---(6|3)
(6)---(5|3)