Thuật toán đường dẫn ngắn nhất nguồn đơn (đối với trọng số không âm) còn được gọi là thuật toán Dijkstra. Có một đồ thị cho trước G (V, E) với biểu diễn ma trận kề của nó và một đỉnh nguồn cũng được cung cấp. Thuật toán Dijkstra để tìm đường đi ngắn nhất nhỏ nhất giữa đỉnh nguồn tới bất kỳ đỉnh nào khác của biểu đồ G.
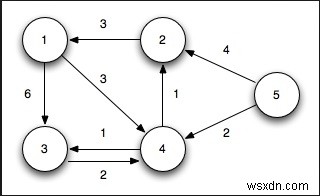
Từ nút bắt đầu đến bất kỳ nút nào khác, hãy tìm khoảng cách nhỏ nhất. Trong bài toán này, đồ thị được biểu diễn bằng ma trận kề. (Ma trận chi phí và ma trận kề tương tự cho mục đích này).
Đầu vào - Ma trận kề -
0 3 6 ∞ ∞ ∞ ∞ 3 0 2 1 ∞ ∞ ∞ 6 2 0 1 4 2 ∞ ∞ 1 1 0 2 ∞ 4 ∞ ∞ 4 2 0 2 1 ∞ ∞ 2 ∞ 2 0 1 ∞ ∞ ∞ 4 1 1 0
Đầu ra -
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
Thuật toán
dijkstraShortestPath (n, dist, next, start)
Đầu vào - Tổng số nút n, danh sách khoảng cách cho mỗi đỉnh, danh sách tiếp theo để lưu trữ nút nào đến tiếp theo và đỉnh gốc hoặc đỉnh bắt đầu.
Đầu ra - Các đường đi ngắn nhất từ đầu đến tất cả các đỉnh khác.
Begin create a status list to hold the current status of the selected node for all vertices u in V do status[u] := unconsidered dist[u] := distance from source using cost matrix next[u] := start done status[start] := considered, dist[start] := 0 and next[start] := φ while take unconsidered vertex u as distance is minimum do status[u] := considered for all vertex v in V do if status[v] = unconsidered then if dist[v] > dist[u] + cost[u,v] then dist[v] := dist[u] + cost[u,v] next[v] := u done done End
Ví dụ (C ++)
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 3, 6, INF, INF, INF, INF},
{3, 0, 2, 1, INF, INF, INF},
{6, 2, 0, 1, 4, 2, INF},
{INF, 1, 1, 0, 2, INF, 4},
{INF, INF, 4, 2, 0, 2, 1},
{INF, INF, 2, INF, 2, 0, 1},
{INF, INF, INF, 4, 1, 1, 0}
};
int minimum(int *status, int *dis, int n){
int i, min, index;
min = INF;
for(i = 0; i<n; i++)
if(dis[i] < min && status[i] == 1){
min = dis[i];
index = i;
}
if(status[index] == 1)
return index;//minimum unconsidered vertex distance
else
return -1;//when all vertices considered
}
void dijkstra(int n, int *dist,int *next, int s){
int status[V];
int u, v;
//initialization
for(u = 0; u<n; u++){
status[u] = 1;//unconsidered vertex
dist[u] = costMat[u][s];//distance from source
next[u] = s;
}
//for source vertex
status[s] = 2; dist[s] = 0; next[s] = -1;//-1 for starting vertex
while((u = minimum(status, dist, n)) > -1){
status[u] = 2;//now considered
for(v = 0; v<n; v++)
if(status[v] == 1)
if(dist[v] > dist[u] + costMat[u][v]){
dist[v] = dist[u] + costMat[u][v];//update distance
next[v] = u;
}
}
}
main(){
int dis[V], next[V], i, start = 0;
dijkstra(V, dis, next, start);
for(i = 0; i<V; i++)
if(i != start)
cout << start << " to " << i <<", Using: " << next[i] << ", Cost: " << dis[i] << endl;
} Đầu ra
0 to 1, Using: 0, Cost: 3 0 to 2, Using: 1, Cost: 5 0 to 3, Using: 1, Cost: 4 0 to 4, Using: 3, Cost: 6 0 to 5, Using: 2, Cost: 7 0 to 6, Using: 4, Cost: 7
