Giả sử chúng ta được cho một đồ thị và được yêu cầu tìm ra 'Cây kéo dài tối thiểu' (MST) từ đồ thị đó. MST của một đồ thị là một tập hợp con của đồ thị có trọng số trong đó tất cả các đỉnh đều có mặt và được nối với nhau, và không tồn tại chu trình trong tập con. MST được gọi là tối thiểu vì tổng trọng số các cạnh của MST là giá trị nhỏ nhất có thể từ đồ thị. Vì vậy, ở đây chúng tôi sử dụng thuật toán MST của Prim và tìm ra tổng trọng số cạnh của MST từ một đồ thị đã cho.
Vì vậy, nếu đầu vào giống như
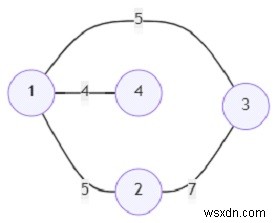
, số đỉnh (n) là 4 và đỉnh bắt đầu (s) =3, thì kết quả đầu ra sẽ là 14.
MST từ biểu đồ này sẽ là cái này -
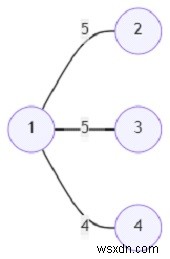
Tổng trọng lượng cạnh của MST này là 14.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một hàm mst_find (). Điều này sẽ lấy G, s
- khoảng cách:=một danh sách mới có kích thước G được khởi tạo với giá trị âm vô cực
- khoảng cách [s]:=0
- itr:=một danh sách mới có kích thước G được khởi tạo với giá trị Sai
- c:=0
- while True, do
- min_weight:=infinity
- m_idx:=-1
- đối với tôi trong phạm vi từ 0 đến kích thước của G, hãy thực hiện
- nếu itr [i] giống với False, thì
- nếu khoảng cách [i]
- min_weight:=distance [i]
- m_idx:=i
- nếu khoảng cách [i]
- nếu itr [i] giống với False, thì
- nếu m_idx giống -1, thì
- ra khỏi vòng lặp
- c:=c + min_weight
- itr [m_idx]:=True
- đối với mỗi cặp i, j trong các giá trị của G [m_idx], thực hiện
- khoảng cách [i]:=tối thiểu của khoảng cách [i], j
- trả lại c
- u:=item [0]
- v:=item [1]
- w:=item [2]
- u:=u - 1
- v:=v - 1
- min_weight =min (G [u, v], w)
- G [u, v]:=min_weight
- G [v, u]:=min_weight
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def mst_find (G, s):distance =[float ("inf")] * len (G) distance [s] =0 itr =[False] * len (G) c =0 while True:min_weight =float ("inf") m_idx =-1 for i in range (len (G)):if itr [i] ==False:if distance [i] Đầu vào
4, [(1, 2, 5), (1, 3, 5), (2, 3, 7), (1, 4, 4)], 3
Đầu ra
14
