Thuật toán của Prim là một thuật toán tham lam tìm cây bao trùm tối thiểu cho một đồ thị vô hướng có trọng số. Nó tìm một tập hợp con của các cạnh tạo thành cây bao gồm mọi đỉnh, trong đó tổng trọng lượng của tất cả các cạnh trong cây được giảm thiểu.
Thuật toán hoạt động bằng cách xây dựng cây này một đỉnh tại một thời điểm, từ một đỉnh bắt đầu tùy ý, ở mỗi bước thêm kết nối rẻ nhất có thể từ cây này sang một đỉnh khác.
Thuật toán của Prim hoạt động như thế nào?
Hãy cùng chúng tôi xem minh họa về cách hoạt động của thuật toán Prim -
1. Chọn một nút bất kỳ làm nút gốc:Trong trường hợp này, chúng ta chọn nút S làm nút gốc của cây khung của Prim. Nút này được chọn tùy ý, vì vậy bất kỳ nút nào cũng có thể là nút gốc. Người ta có thể thắc mắc tại sao bất kỳ video nào cũng có thể là một nút gốc. Vì vậy, câu trả lời là, trong cây khung tất cả các nút của biểu đồ đều được bao gồm và vì nó được kết nối nên phải có ít nhất một cạnh, cạnh này sẽ nối nó với phần còn lại của cây.
2. Kiểm tra các cạnh đi và chọn một cạnh có giá trị nhỏ hơn:Sau khi chọn nút gốc S, ta thấy S, A và S, C là hai cạnh có trọng số lần lượt là 7 và 8. Chúng tôi chọn cạnh S, A vì nó nhỏ hơn cạnh kia.
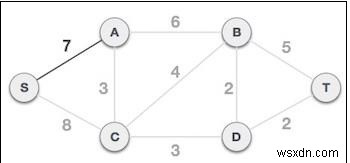
Bây giờ, cây S-7-A được coi như một nút và chúng tôi kiểm tra tất cả các cạnh đi ra khỏi nó. Chúng tôi chọn loại có chi phí thấp nhất và đưa vào cây.
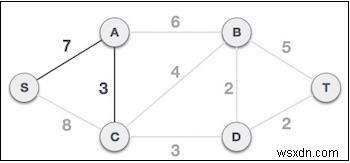
Sau bước này, cây S-7-A-3-C được hình thành. Bây giờ chúng ta sẽ lại coi nó như một nút và sẽ kiểm tra lại tất cả các cạnh. Tuy nhiên, chúng tôi sẽ chỉ chọn cạnh có chi phí thấp nhất. Trong trường hợp này, C-3-D là cạnh mới, thấp hơn giá của các cạnh khác 8, 6, 4, v.v.
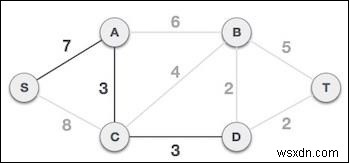
Sau khi thêm nút D đối với cây khung, bây giờ chúng ta có hai cạnh đi ra khỏi nó có cùng chi phí, tức là D-2-T và D-2-B. Do đó, chúng ta có thể thêm một trong hai. Nhưng bước tiếp theo sẽ mang lại cạnh 2 là chi phí ít nhất. Do đó, chúng tôi đang hiển thị một cây khung bao gồm cả hai cạnh.
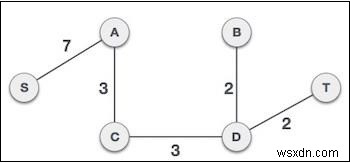
Bây giờ hãy để chúng tôi xem cách chúng tôi có thể triển khai tương tự trong mã của chúng tôi -
Ví dụ
primsMST() {
// Initialize graph that'll contain the MST
const MST = new Graph();
if (this.nodes.length === 0) {
return MST;
}
// Select first node as starting node
let s = this.nodes[0];
// Create a Priority Queue and explored set
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
let explored = new Set();
explored.add(s);
MST.addNode(s);
// Add all edges from this starting node to the PQ taking weights as priority
this.edges[s].forEach(edge => {
edgeQueue.enqueue([s, edge.node], edge.weight);
});
// Take the smallest edge and add that to the new graph
let currentMinEdge = edgeQueue.dequeue();
while (!edgeQueue.isEmpty()) {
// COntinue removing edges till we get an edge with an unexplored node
while (!edgeQueue.isEmpty() && explored.has(currentMinEdge.data[1])) {
currentMinEdge = edgeQueue.dequeue();
}
let nextNode = currentMinEdge.data[1];
// Check again as queue might get empty without giving back unexplored element
if (!explored.has(nextNode)) {
MST.addNode(nextNode);
MST.addEdge(currentMinEdge.data[0], nextNode, currentMinEdge.priority);
// Again add all edges to the PQ
this.edges[nextNode].forEach(edge => {
edgeQueue.enqueue([nextNode, edge.node], edge.weight);
});
// Mark this node as explored explored.add(nextNode);
s = nextNode;
}
}
return MST;
} Bạn có thể kiểm tra điều này bằng cách sử dụng:
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C", 100);
g.addEdge("A", "B", 3);
g.addEdge("A", "D", 4);
g.addEdge("C", "D", 3);
g.addEdge("D", "E", 8);
g.addEdge("E", "F", 10);
g.addEdge("B", "G", 9);
g.primsMST().display(); Đầu ra
Điều này sẽ cung cấp đầu ra -
A->B, D B->A, G D->A, C, E C->D E->D, F G->B F->E
Lưu ý rằng biểu đồ Ban đầu của chúng tôi là -
Ví dụ
/** * A * / | \ * C | B * \ | | * D G * | / * E * | * F */
Đầu ra
Biểu đồ hiện tại của chúng tôi trông giống như -
/** * A * |\ * C | B * \ | | * D G * | * E * | * F * */
Chúng tôi đã loại bỏ các cạnh đắt nhất và bây giờ có một cây bao trùm.
