Xoay AVL trong Javascript

Để tự cân bằng, cây AVL có thể thực hiện bốn kiểu xoay sau -

• Xoay trái
• Xoay phải
• Xoay trái-phải
• Xoay phải-trái

Hai phép quay đầu tiên là phép quay đơn và hai phép quay tiếp theo là phép quay kép. Để có một cây không cân đối, ít nhất chúng ta cần một cây cao 2. Với cây đơn giản này, chúng ta hãy hiểu từng cây một.

Xoay trái

Nếu một cây trở nên không cân bằng, khi một nút được chèn vào cây con bên phải của cây con bên phải, thì chúng ta thực hiện một phép quay trái duy nhất -

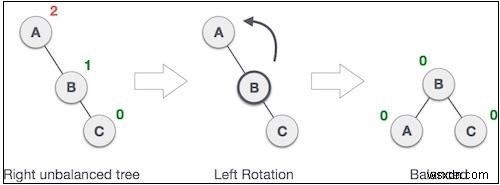
Trong ví dụ của chúng tôi, nút A đã trở nên không cân bằng khi một nút được chèn vào cây con bên phải của cây con bên phải của A. Chúng tôi thực hiện xoay trái bằng cách thực hiện A cây con bên trái của B . Vòng quay này còn được gọi là vòng quay LL. Hãy để chúng tôi xem cách chúng tôi có thể triển khai nó -

function rotationLL(node) {
let tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}

Xoay phải

Cây AVL có thể trở nên không cân bằng nếu một nút được chèn vào cây con bên trái của cây con bên trái. Sau đó, cây cần phải xoay vòng.

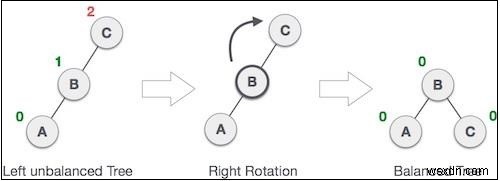
Như mô tả, nút không cân bằng trở thành nút con bên phải của nút con bên trái của nó bằng cách thực hiện quay phải. Đây còn được gọi là vòng quay RR. Hãy để chúng tôi xem nó trông như thế nào trong mã -

function rotationRR(node) {
let tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}

Xoay trái-phải

Phép quay kép là một phiên bản hơi phức tạp của các phiên bản xoay đã được giải thích. Để hiểu rõ hơn về chúng, chúng ta nên lưu ý từng hành động được thực hiện trong khi xoay. Đầu tiên chúng ta hãy kiểm tra cách thực hiện xoay Trái-Phải. Xoay trái-phải là sự kết hợp của xoay trái và xoay phải.

Trạng thái	Hành động
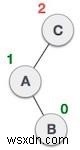	Một nút đã được chèn vào cây con bên phải của cây con bên trái. Điều này làm cho C một nút không cân bằng. Các trường hợp này khiến cây AVL thực hiện xoay trái-phải.
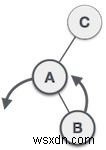	Đầu tiên chúng tôi thực hiện xoay trái trên cây con bên trái của C. Điều này làm cho A , cây con bên trái của B .
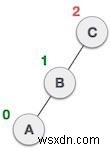	C vẫn không cân bằng, tuy nhiên bây giờ, đó là do cây con bên trái của cây con bên trái.
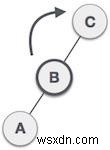	Bây giờ chúng ta sẽ xoay cây sang phải, tạo B nút gốc mới của cây con này. C bây giờ trở thành cây con bên phải của cây con bên trái của chính nó.
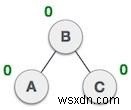	Cây hiện đã được cân bằng.

Đây cũng được gọi là một vòng quay LR vì lần đầu tiên chúng ta thực hiện một vòng quay bên trái, sau đó là một vòng quay bên phải. Điều này có thể được thực hiện bằng 2 phương pháp trước như sau -

function rotationLR(node) {
node.left = rotationRR(node.left);
return rotationLL(node);
}

Xoay phải-trái

Kiểu quay kép thứ hai là Xoay phải-Trái. Nó là sự kết hợp của xoay phải sau đó là xoay trái.

Trạng thái	Hành động
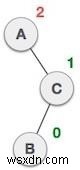	Một nút đã được chèn vào cây con bên trái của cây con bên phải. Điều này làm cho A, một nút không cân bằng với hệ số cân bằng 2.
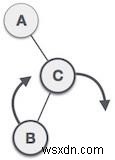	Đầu tiên, chúng tôi thực hiện xoay bên phải dọc theo C nút, tạo C cây con bên phải của cây con bên trái của chính nó B . Bây giờ, B trở thành cây con bên phải của A .
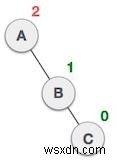	A vẫn không cân bằng vì cây con bên phải của cây con bên phải của nó và yêu cầu xoay trái.
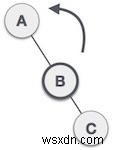	Xoay trái được thực hiện bằng cách thực hiện B nút gốc mới của cây con. Đ trở thành cây con bên trái của cây con bên phải B .
	Cây hiện đã được cân bằng.

Đây cũng được gọi là một vòng quay RL vì đầu tiên chúng ta thực hiện một vòng quay bên phải, sau đó là một vòng quay bên trái. Điều này có thể được thực hiện bằng 2 phương pháp trước như sau -

function rotationRL(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}