Chương trình tìm cấp cây có tổng tối thiểu trong C ++

Giả sử chúng ta có một cây nhị phân, cấp của gốc là 1, cấp con của nó là 2, v.v. Chúng ta phải tìm cấp X nhỏ nhất sao cho tổng tất cả các giá trị của các nút ở cấp X là nhỏ nhất. Vì vậy, nếu cây như -

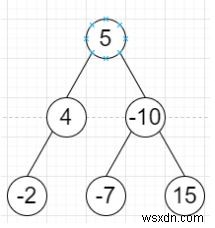
Đầu ra sẽ là 2 vì tổng là 4 - 10 =-6, là nhỏ nhất.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

level:=1, sum:=value of r, ansLevel:=level, ansSum:=sum
xác định hàng đợi q, chèn nút r đã cho vào q
trong khi q không trống
- công suất:=kích thước của q
- tăng cấp 1, sum:=0
- trong khi dung lượng không bằng 0
  - node:=front node from q, delete node from q
  - nếu bên phải của nút hợp lệ, thì sum:=sum + giá trị của nút bên phải, chèn bên phải
  - nút thành q
  - nếu bên trái của nút là hợp lệ, thì sum:=sum + giá trị của nút bên trái, chèn nút bên trái vào q
  - giảm công suất 1
- nếu ansSum
trả về ansLevel

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn−

Ví dụ

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
   public:
      int val;
      TreeNode *left, *right;
      TreeNode(int data){
         val = data;
         left = NULL;
      right = NULL;
      }
};
class Solution {
   public:
   int solve(TreeNode* r) {
      int level = 1, sum = r->val;
      int ansLevel = level, ansSum = sum;
      queue <TreeNode*> q;
      q.push(r);
      while(!q.empty()){
         int capacity = q.size();
         level++;
         sum = 0;
         while(capacity--){
            TreeNode* node = q.front();
            q.pop();
            if(node->right){
               sum += node->right->val;
               q.push(node->right);
            }
            if(node->left){
               sum += node->left->val;
               q.push(node->left);
            }
         }
         if(ansSum>sum){
            ansSum = sum;
            ansLevel = level;
         }
      }
      return ansLevel;
   }
};
main(){
   TreeNode *root = new TreeNode(5);
   root->left = new TreeNode(4);
   root->right = new TreeNode(-10);
   root->left->right = new TreeNode(-2);
   root->right->left = new TreeNode(-7);
   root->right->right = new TreeNode(15);
   Solution ob;
   cout <<ob.solve(root);
}

Đầu vào

TreeNode *root = new TreeNode(5);
root->left = new TreeNode(4);
root->right = new TreeNode(-10);
root->left->right = new TreeNode(-2);
root->right->left = new TreeNode(-7);
root->right->right = new TreeNode(15);