Giới thiệu về Hồi quy tuyến tính
Khái niệm cơ bản về hồi quy tuyến tính đơn giản
-
Cho phép chúng tôi hiểu mối quan hệ giữa hai biến liên tục.
-
Ví dụ -
-
x =biến độc lập
-
trọng lượng
-
-
y =biến phụ thuộc
-
chiều cao
-
-
-
y =αx + β
Hãy hiểu hồi quy tuyến tính đơn giản thông qua một chương trình -
#Simple linear regression import numpy as np import matplotlib.pyplot as plt np.random.seed(1) n = 70 x = np.random.randn(n) y = x * np.random.randn(n) colors = np.random.rand(n) plt.plot(np.unique(x), np.poly1d(np.polyfit(x, y, 1))(np.unique(x))) plt.scatter(x, y, c = colors, alpha = 0.5) plt.show()
Đầu ra
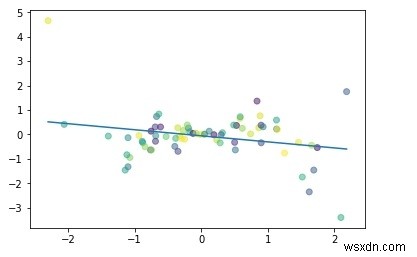
Mục đích của Hồi quy tuyến tính:
-
để Giảm thiểu khoảng cách giữa các điểm và đường thẳng (y =αx + β)
-
Điều chỉnh
-
Hệ số:α
-
Đánh chặn / Độ lệch:β
-
Xây dựng Mô hình hồi quy tuyến tính với PyTorch
Giả sử hệ số của chúng ta (α) là 2 và hệ số chặn (β) là 1 thì phương trình của chúng ta sẽ trở thành -
y =2x +1 mô hình #Linear
Xây dựng Tập dữ liệu
x_values = [i for i in range(11)] x_values
Đầu ra
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# chuyển đổi thành numpy
x_train = np.array(x_values, dtype = np.float32) x_train.shape
Đầu ra
(11,)
#Important: 2D required x_train = x_train.reshape(-1, 1) x_train.shape
Đầu ra
(11, 1)
y_values = [2*i + 1 for i in x_values] y_values
Đầu ra
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
#list iteration y_values = [] for i in x_values: result = 2*i +1 y_values.append(result) y_values
Đầu ra
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
y_train = np.array(y_values, dtype = np.float32) y_train.shape
Đầu ra
(11,)
#2D required y_train = y_train.reshape(-1, 1) y_train.shape
Đầu ra
(11, 1)
Mô hình xây dựng
#import libraries
import torch
import torch.nn as nn
from torch.autograd import Variable
#Create Model class
class LinearRegModel(nn.Module):
def __init__(self, input_size, output_size):
super(LinearRegModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = 1
output_dim = 1
model = LinearRegModel(input_dim, output_dim)
criterion = nn.MSELoss()
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr = learning_rate)
epochs = 100
for epoch in range(epochs):
epoch += 1
#convert numpy array to torch variable
inputs = Variable(torch.from_numpy(x_train))
labels = Variable(torch.from_numpy(y_train))
#Clear gradients w.r.t parameters
optimizer.zero_grad()
#Forward to get output
outputs = model.forward(inputs)
#Calculate Loss
loss = criterion(outputs, labels)
#Getting gradients w.r.t parameters
loss.backward()
#Updating parameters
optimizer.step()
print('epoch {}, loss {}'.format(epoch, loss.data[0])) Đầu ra
epoch 1, loss 276.7417907714844 epoch 2, loss 22.601360321044922 epoch 3, loss 1.8716105222702026 epoch 4, loss 0.18043726682662964 epoch 5, loss 0.04218350350856781 epoch 6, loss 0.03060017339885235 epoch 7, loss 0.02935197949409485 epoch 8, loss 0.02895027957856655 epoch 9, loss 0.028620922937989235 epoch 10, loss 0.02830091118812561 ...... ...... epoch 94, loss 0.011018744669854641 epoch 95, loss 0.010895680636167526 epoch 96, loss 0.010774039663374424 epoch 97, loss 0.010653747245669365 epoch 98, loss 0.010534750297665596 epoch 99, loss 0.010417098179459572 epoch 100, loss 0.010300817899405956
Vì vậy, chúng ta có thể giảm đáng kể tổn thất từ kỷ nguyên 1 xuống kỷ nguyên 100.
Vẽ biểu đồ
#Purely inference predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() predicted y_train #Plot Graph #Clear figure plt.clf() #Get predictions predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() #Plot true data plt.plot(x_train, y_train, 'go', label ='True data', alpha = 0.5) #Plot predictions plt.plot(x_train, predicted, '--', label='Predictions', alpha = 0.5) #Legend and Plot plt.legend(loc = 'best') plt.show()
Đầu ra
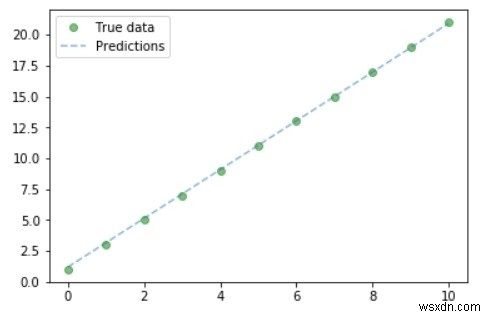
Vì vậy, chúng ta có thể từ biểu đồ - giá trị thực và dự đoán của chúng ta gần như tương tự nhau.
