Hồi quy tuyến tính là một trong những công cụ tiêu chuẩn đơn giản nhất trong học máy để chỉ ra liệu có mối quan hệ tích cực hay tiêu cực giữa hai biến.
Hồi quy tuyến tính là một trong số ít công cụ tốt để phân tích dự đoán nhanh chóng. Trong phần này, chúng ta sẽ sử dụng gói python pandas để tải dữ liệu và sau đó ước tính, diễn giải và trực quan hóa các mô hình hồi quy tuyến tính.
Trước khi đi sâu hơn, trước tiên hãy thảo luận về hồi quy là gì?
Hồi quy là gì?
Hồi quy là một dạng của kỹ thuật mô hình dự đoán giúp tạo ra mối quan hệ giữa biến phụ thuộc và biến độc lập.
Các loại hồi quy
- Hồi quy tuyến tính
- Hồi quy logistic
- Hồi quy đa thức
- Hồi quy từng bước
Hồi quy tuyến tính được sử dụng ở đâu?
- Đánh giá Xu hướng và Ước tính Doanh số
- Phân tích tác động của việc thay đổi giá
- Đánh giá rủi ro
Các bước xây dựng mô hình hồi quy tuyến tính của chúng tôi
-
Trước tiên, chúng tôi sẽ xây dựng thiết lập và tải xuống tập dữ liệu và jupyter (tôi đang sử dụng cho hướng dẫn này, bạn có thể sử dụng IDE khác như anaconda hoặc tương tự).
-
Nhập gói và tập dữ liệu được yêu cầu.
-
Khi đã tải xong tập dữ liệu, chúng tôi sẽ khám phá tập dữ liệu của mình.
-
Sẽ thực hiện hồi quy tuyến tính với tập dữ liệu của chúng tôi
-
Sau đó, chúng ta sẽ khám phá mối quan hệ giữa biến của chúng ta và Thời gian trong ngày.
-
Tóm tắt.
Thiết lập
Bạn có thể tải xuống bộ dữ liệu từ liên kết dưới đây,
http://en.openei.org/datasets/dataset/649aa6d3-2832-4978-bc6e-fa563568398e/resource/b710e97d-29c9-4ca5-8137-63b7cf447317/download/building1retail.csv
mà chúng tôi sẽ sử dụng để mô hình hóa sức mạnh của một tòa nhà bằng cách sử dụng Nhiệt độ không khí ngoài trời (OAT) như một biến giải thích.
Lưu tệp csv trong cùng một thư mục nơi jupyter hoặc IDE của chúng tôi được cài đặt.
Nhập các thư viện và tập dữ liệu Bắt buộc
Đầu tiên, chúng ta sẽ nhập các thư viện cần thiết và sau đó đọc tập dữ liệu bằng thư viện pandas python.
# Importing Necessary Libraries
import pandas as pd
#Required for numerical functions
import numpy as np
from scipy import stats
from datetime import datetime
from sklearn import preprocessing
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
#For plotting the graph
import matplotlib.pyplot as plt
%matplotlib inline
# Reading Data
df = pd.read_csv('building1retail.csv', index_col=[0],
date_parser=lambda x: datetime.strptime(x, "%m/%d/%Y %H:%M"))
df.head() Đầu ra

Khám phá tập dữ liệu
Vì vậy, trước tiên hãy hình dung tập dữ liệu của chúng tôi bằng cách vẽ biểu đồ với gấu trúc.
df.plot(figsize=(22,6))
Đầu ra
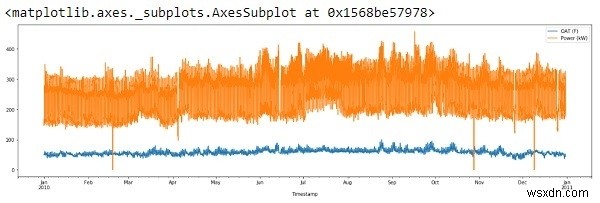
Vì vậy, trục x đang hiển thị dữ liệu từ tháng 1 năm 2010 - tháng 1 năm 2011.
Nếu chúng ta thấy kết quả ở trên, chúng ta có thể nhận thấy có hai điều kỳ lạ về cốt truyện:
-
Dường như không có dữ liệu nào bị thiếu, Để kiểm tra, chỉ cần chạy:
df.isnull().values.any()
Đầu ra
False
Kết quả sai cho chúng ta biết không có giá trị null nào trong khung dữ liệu.
-
Dường như, có một số điểm bất thường trong dữ liệu (mức tăng đột biến dài xuống)
Các điểm bất thường hoặc 'ngoại lệ' thường là kết quả của một lỗi thử nghiệm hoặc có thể là giá trị thực. Trong cả hai trường hợp, chúng tôi sẽ loại bỏ nó vì chúng ảnh hưởng nghiêm trọng đến độ dốc của đường hồi quy.
Trước khi chúng tôi loại bỏ các 'ngoại lệ', trước tiên hãy kiểm tra xem dữ liệu của chúng tôi đang đại diện cho loại phân phối nào:
df.hist()
Đầu ra
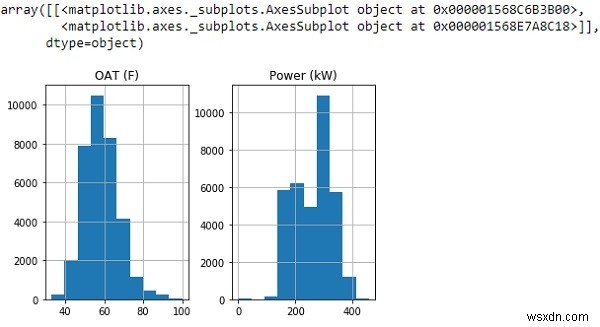
Từ biểu đồ trên, chúng ta có thể thấy biểu đồ của mình đang hiển thị dữ liệu gần như tuân theo phân phối chuẩn.
Vì vậy, hãy loại bỏ tất cả các giá trị lớn hơn 3 độ lệch chuẩn so với giá trị trung bình và vẽ biểu đồ khung dữ liệu mới.
std_dev = 3 df = df[(np.abs(stats.zscore(df)) < float(std_dev)).all(axis=1)] df.plot(figsize=(22, 6))
Đầu ra
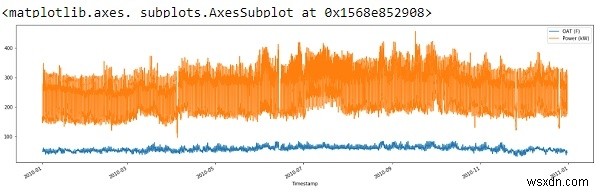
Vì vậy, từ đầu ra ở trên, chúng ta có thể thấy, chúng tôi đã loại bỏ các gai ở một mức độ nào đó và làm sạch dữ liệu của mình.
Xác thực mối quan hệ tuyến tính
Để tìm xem có bất kỳ mối quan hệ tuyến tính nào giữa OAT và Power hay không, hãy vẽ một biểu đồ phân tán đơn giản:
plt.scatter(df['OAT (F)'], df['Power (kW)'])
Đầu ra
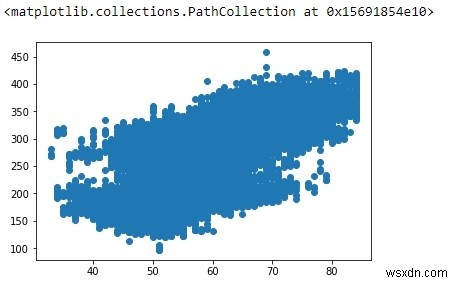
Hồi quy tuyến tính
Để chạy các mô hình và đánh giá hiệu suất của nó, chúng tôi cũng sẽ sử dụng mô-đun Scikit-learning, chúng tôi sẽ sử dụng xác thực chéo k-nếp gấp (k =3) để đánh giá hiệu suất của mô hình của chúng tôi.
X = pd.DataFrame(df['OAT (F)']) y = pd.DataFrame(df['Power (kW)']) model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) score = model.score(X.iloc[test,:], y.iloc[test,:]) scores.append(score) print(scores)
Đầu ra
[0.38768927735902703, 0.3852220878090444, 0.38451654781487116]
Trong chương trình trên, model =LinearRegression () tạo ra một mô hình hồi quy tuyến tính và vòng lặp for chia tập dữ liệu thành ba lần. Sau đó, bên trong vòng lặp, chúng tôi phù hợp với dữ liệu và sau đó đánh giá hiệu suất của nó bằng cách thêm điểm của nó vào một danh sách.
Tuy nhiên, kết quả có vẻ không tốt và chúng tôi có thể cải thiện hiệu suất của nó.
Thời gian trong ngày
Công suất (biến) phụ thuộc nhiều vào thời gian trong ngày. Hãy sử dụng thông tin này để kết hợp nó vào mô hình hồi quy của chúng tôi bằng cách sử dụng mã hóa một lần.
model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) scores.append(model.score(X.iloc[test,:], y.iloc[test,:])) print(scores)
Đầu ra
[0.8074246958895391, 0.8139449185141592, 0.8111379602960773]
Đó là sự khác biệt lớn mà chúng tôi có trong mô hình của mình.
Tóm tắt
Trong phần này, chúng ta đã học những kiến thức cơ bản về cách khám phá tập dữ liệu và chuẩn bị nó để phù hợp với mô hình hồi quy. Chúng tôi đã đánh giá hiệu suất của nó, phát hiện những thiếu sót và khắc phục nó.
