Quy tắc hình thang cho tích phân xác định

Tích phân xác định có thể được giải bằng cách sử dụng quy tắc hình thang này. Để tích phân một hàm f (x) giữa phạm vi từ a đến b về cơ bản là tìm vùng bên dưới đường cong từ điểm x =a đến x =b.

Để tìm diện tích đó, ta có thể chia diện tích thành n hình thang và chiều rộng của mỗi hình thang là h, do đó ta có thể nói rằng (b - a) =nh. Khi số lượng hình thang tăng lên thì kết quả tính diện tích sẽ chính xác hơn. Để giải tích phân, chúng ta sẽ làm theo công thức này.

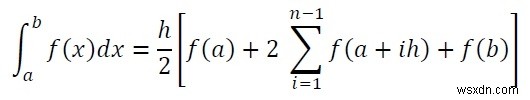
Ở đây h là độ rộng của khoảng và n là số khoảng. Chúng ta có thể tìm thấy chữ h bằng cách sử dụng

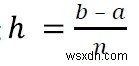
Đầu vào và Đầu ra

Input:
The function f(x): 1-exp(-x/2.0) and limits of the integration: 0, 1. The number of intervals: 20
Output:
The answer is: 0.21302

Thuật toán

integrateTrapezoidal(a, b, n)

Đầu vào: Giới hạn dưới và giới hạn trên, và số lượng các tích phân n.

Đầu ra: Kết quả của tích hợp.

Begin
   h := (b - a)/n
   sum := f(a) + f(b)
   for i := 1 to n, do
      sum := sum + f(a + ih)
   done
   return sum
End

Ví dụ

#include<iostream>
#include<cmath>
using namespace std;

float mathFunc(float x) {
   return (1-exp(-x/2.0));    //the function 1 - e^(-x/2)
}

float integrate(float a, float b, int n) {
   float h, sum;
   int i;
   h = (b-a)/n;    //calculate the distance between two interval
   sum = (mathFunc(a)+mathFunc(b))/2;    //initial sum using f(a) and f(b)

   for(i = 1; i<n; i++) {
      sum += mathFunc(a+i*h);
   }
   return (h*sum);    //The result of integration
}

main() {
   float result, lowLim, upLim;
   int interval;
   cout << "Enter Lower Limit, Upper Limit and interval: "; cin >>lowLim >>upLim >>interval;
   result = integrate(lowLim, upLim, interval);
   cout << "The answer is: " << result;
}

Đầu ra

Enter Lower Limit, Upper Limit and interval: 0 1 20
The answer is: 0.21302