Quy tắc 1/3 của Simpson cho tích phân xác định

Giống như Quy tắc Hình thang, Quy tắc 1/3 của Simpson cũng được sử dụng để tìm giá trị tích phân từ phạm vi a đến b. Sự khác biệt chính giữa hình thang và quy tắc Simpson’s 1/3 là, trong quy tắc hình thang, toàn bộ phần được chia thành một số hình thang, nhưng trong trường hợp này, mỗi hình thang cũng được chia thành hai phần.

Đối với quy tắc này, chúng tôi sẽ làm theo công thức sau:

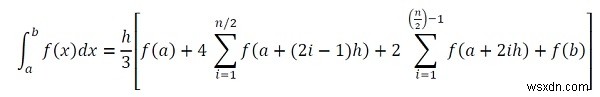
Ở đây h là độ rộng của khoảng và n là số khoảng. Chúng ta có thể tìm thấy chữ h bằng cách sử dụng

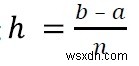
Đầu vào và Đầu ra

Input:
The function f(x): (x+(1/x). The lower and upper limit: 1, 2. The number of intervals: 20.
Output:
The answer is: 2.19315

Thuật toán

integrateSimpson(a, b, n)

Đầu vào - Giới hạn dưới và giới hạn trên của tích phân và số khoảng n.

Đầu ra - Kết quả sau khi tích hợp.

Begin
   h := (b - a)/n
   res := f(a) + f(b)
   lim := n/2

   for i := 1 to lim, do
      oddSum := oddSum + f(a + (2i - 1)h)
   done

   oddSum := oddSum * 4
   for i := 1 to lim-1, do
      evenSum := evenSum + f(a + 2ih)
   done

   evenSum := evenSum * 2
   res := res + oddSum + evenSum
   res := res * (h/3)
   return res
End

Ví dụ

#include<iostream>
#include<cmath>
using namespace std;

float mathFunc(float x) {
   return (x+(1/x));    //function 1 + 1/x
}

float integrate(float a, float b, int n) {
   float h, res = 0.0, oddSum = 0.0, evenSum = 0.0, lim;
   int i;
   h = (b-a)/n;    //calculate the distance between two interval
   res = (mathFunc(a)+mathFunc(b));    //initial sum using f(a) and f(b)
   lim = n/2;

   for(i = 1; i<=lim; i++)
      oddSum += mathFunc(a+(2*i-1)*h);    //sum of numbers, placed at odd number
   oddSum *= 4;    //odd sum are multiplied by 4

   for(i = 1; i<lim; i++)
      evenSum += mathFunc(a+(2*i)*h);    //sum of numbers, placed at even number
   evenSum *= 2;    //even sum are multiplied by 2
   res += oddSum+evenSum;
   res *= (h/3);
   return res;    //The result of integration
}

main() {
   float result, lowLim, upLim;
   int interval;
   cout << "Enter Lower Limit, Upper Limit and interval: ";
   cin >>lowLim >>upLim >>interval;
   result = integrate(lowLim, upLim, interval);
   cout << "The answer is: " << result;
}

Đầu ra

Enter Lower Limit, Upper Limit and interval: 1 2 20
The answer is: 2.19315