Tìm kiếm độ sâu đầu tiên (DFS) cho một biểu đồ

Tìm kiếm theo độ sâu-đầu tiên (DFS) là một thuật toán duyệt đồ thị. Trong thuật toán này, một đỉnh bắt đầu được đưa ra và khi một đỉnh liền kề được tìm thấy, nó sẽ di chuyển đến đỉnh liền kề đó trước tiên và cố gắng đi ngang theo cách tương tự.

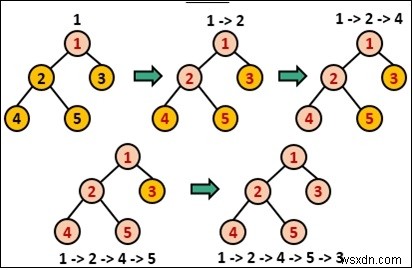
Nó di chuyển qua toàn bộ độ sâu, hết mức có thể, sau đó nó quay trở lại các đỉnh trước đó để tìm con đường mới.

Để triển khai DFS theo cách lặp lại, chúng ta cần sử dụng cấu trúc dữ liệu ngăn xếp. Nếu chúng ta muốn thực hiện điều đó một cách đệ quy, thì không cần các ngăn xếp bên ngoài, nó có thể được thực hiện ngăn xếp bên trong cho các cuộc gọi đệ quy.

Đầu vào và Đầu ra

Input:
The Adjacency matrix of a graph.
 
        A B C D E F
      A 0 1 1 1 0 0
      B 1 0 0 1 1 0
      C 1 0 0 1 1 0
      D 1 1 1 0 1 1
      E 0 1 0 1 0 1
      F 0 0 1 1 1 0

Output:
DFS Traversal: C F E B D A

Thuật toán

dfs(vertices, start)

Đầu vào: Danh sách tất cả các đỉnh và nút bắt đầu.

Đầu ra: Duyệt qua tất cả các nút trong biểu đồ.

Begin
   initially make the state to unvisited for all nodes
   push start into the stack

   while stack is not empty, do
      pop element from stack and set to u
      display the node u

      if u is not visited, then
         mark u as visited
         for all nodes i connected to u, do
            if ith vertex is unvisited, then
               push ith vertex into the stack
               mark ith vertex as visited
         done
   done
End

Ví dụ

#include<iostream>
#include<stack>
using namespace std;
#define NODE 6

typedef struct node {
   int val;
   int state; //status
}node;

int graph[NODE][NODE] = {
   {0, 1, 1, 1, 0, 0},
   {1, 0, 0, 1, 1, 0},
   {1, 0, 0, 1, 0, 1},
   {1, 1, 1, 0, 1, 1},
   {0, 1, 0, 1, 0, 1},
   {0, 0, 1, 1, 1, 0}
};

void dfs(node *vertex, node start) {
   node u;
   stack<node> myStack;

   for(int i = 0; i<NODE; i++) {
      vertex[i].state = 0;   //not visited
   }

   myStack.push(start);
   while(!myStack.empty()) {
      //pop and print node
      u = myStack.top();
      myStack.pop();
      cout << char(u.val+'A') << " ";

      if(u.state != 1) {
         //update vertex status to visited
         u.state = 1;
         vertex[u.val].state = 1;

         for(int i = 0; i<NODE; i++) {
            if(graph[i][u.val]) {
               if(vertex[i].state == 0) {
                  myStack.push(vertex[i]);
                  vertex[i].state = 1;
               }
            }
         }
      }
   }
}

int main() {
   node vertices[NODE];
   node start;
   char s;

   for(int i = 0; i<NODE; i++) {
      vertices[i].val = i;
   }

   s = 'C';   //starting vertex C
   start.val = s-'A';
   cout << "DFS Traversal: ";
   dfs(vertices, start);
   cout << endl;
}

Đầu ra

DFS Traversal: C F E B D A