Vấn đề tô màu M

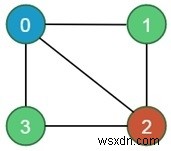
Trong bài toán này, một đồ thị vô hướng được đưa ra. Ngoài ra còn có m màu được cung cấp. Vấn đề là tìm xem có thể gán các nút có m màu khác nhau sao cho không có hai đỉnh kề nhau của đồ thị có cùng màu hay không. Nếu giải pháp tồn tại, thì hiển thị màu nào được chỉ định trên đỉnh nào.

Bắt đầu từ đỉnh 0, chúng ta sẽ cố gắng gán từng màu một cho các nút khác nhau. Nhưng trước khi ấn định phải kiểm tra xem màu có an toàn hay không. Một màu không an toàn cho dù các đỉnh liền kề có chứa cùng một màu hay không.

Đầu vào và Đầu ra

Input:
The adjacency matrix of a graph G(V, E) and an integer m, which indicates the maximum number of colors that can be used.


Let the maximum color m = 3.
Output:
This algorithm will return which node will be assigned with which color. If the solution is not possible, it will return false.
For this input the assigned colors are:
Node 0 -> color 1
Node 1 -> color 2
Node 2 -> color 3
Node 3 -> color 2

Thuật toán

isValid (đỉnh, colorList, col)

Đầu vào - Vertex, colorList để kiểm tra và màu đang cố gắng gán.

Đầu ra - Đúng nếu việc gán màu hợp lệ, ngược lại là sai.

Begin
   for all vertices v of the graph, do
      if there is an edge between v and i, and col = colorList[i], then
         return false
   done
   return true
End

graphColoring (màu sắc, colorList, đỉnh)

Đầu vào - Hầu hết các màu có thể có, danh sách các đỉnh được tô với màu nào và đỉnh bắt đầu.

Đầu ra - Đúng, khi màu sắc được chỉ định, nếu không, sai.

Begin
   if all vertices are checked, then
      return true
   for all colors col from available colors, do
      if isValid(vertex, color, col), then
         add col to the colorList for vertex
         if graphColoring(colors, colorList, vertex+1) = true, then
            return true
         remove color for vertex
   done
   return false
End

Ví dụ

#include<iostream>
#define V 4
using namespace std;

bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0},
};

void showColors(int color[]) {
   cout << "Assigned Colors are: " <<endl;
   for (int i = 0; i < V; i++)
      cout << color[i] << " ";
   cout << endl;
}

bool isValid(int v,int color[], int c) {    //check whether putting a color valid for v
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}

bool graphColoring(int colors, int color[], int vertex) {
   if (vertex == V)    //when all vertices are considered
      return true;

   for (int col = 1; col <= colors; col++) {
      if (isValid(vertex,color, col)) {     //check whether color col is valid or not
         color[vertex] = col;
         if (graphColoring (colors, color, vertex+1) == true)    //go for additional vertices
            return true;
                   
         color[vertex] = 0;
      }
   }
   return false; //when no colors can be assigned
}

bool checkSolution(int m) {
   int *color = new int[V];    //make color matrix for each vertex

   for (int i = 0; i < V; i++)
      color[i] = 0;      //initially set to 0

   if (graphColoring(m, color, 0) == false) {    //for vertex 0 check graph coloring
      cout << "Solution does not exist.";
      return false;
   }
   showColors(color);
   return true;
}

int main() {
   int colors = 3;      // Number of colors
   checkSolution (colors);
}

Đầu ra

Assigned Colors are:
1 2 3 2