Phương pháp bí mật để giải phương trình phi tuyến tính

Phương pháp Secant cũng được sử dụng để giải các phương trình phi tuyến tính. Phương pháp này tương tự như phương pháp Newton-Raphson, nhưng ở đây chúng ta không cần tìm phân biệt của hàm f (x). Chỉ sử dụng f (x), chúng ta có thể tìm f ’(x) ở dạng số bằng cách sử dụng công thức sai phân Newton’s Chia. Từ công thức Newton-Raphson,

chúng tôi biết điều đó,

Bây giờ, sử dụng công thức chênh lệch số chia, chúng tôi nhận được,

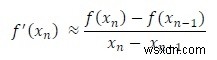
Bằng cách thay thế f ’(x) của công thức Newton-Raphson bằng f’ (x) mới, chúng ta có thể tìm thấy công thức secant để giải các phương trình phi tuyến tính.

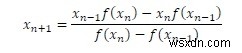
Lưu ý: Đối với phương pháp này, chúng ta cần hai lần phỏng đoán ban đầu bất kỳ để bắt đầu tìm gốc của phương trình phi tuyến tính.

Đầu vào và Đầu ra

Input:
The function f(x) = (x*x) - (4*x) - 10
Output:
The root is: -1.74166

Thuật toán

secant(x1, x2)

Đầu vào: Hai dự đoán ban đầu cho root.

Đầu ra: Căn gần đúng của phương trình phi tuyến tính f (x).

Begin
   f1 := f(x1)
   f2 := f(x2)
   x3 := ((f2*x1) – (f1*x2)) / (f2 – f1)
   while relative error of x3 and x2 are > precision, do
      x1 := x2
      f1 := f2
      x2 := x3
      f2 := f(x2)
      x3 := ((f2*x1) – (f1*x2)) / (f2 – f1)
   done
   root := x3
   return root
End

Ví dụ

#include<iostream>
#include<cmath>
using namespace std;

double absolute(double value) {             //to find magnitude of value
   if(value < 0)
      return (-value);
   return value;
}

double f(double x) {              //the given function x^2-4x-10
   return ((x*x)-(4*x)-10);
}

double secant(double x1, double x2) {
   double x3, root;
   double f1, f2;
   f1 = f(x1);
   f2 = f(x2);
   x3 = (f2*x1-f1*x2)/(f2-f1);

   while(absolute((x3-x2)/x3) > 0.00001) {         //test accuracy of x3
      x1 = x2;           //shift x values
      f1 = f2;
      x2 = x3;
      f2 = f(x2);                 //find new x2
      x3 = (f2*x1-f1*x2)/(f2-f1);          //calculate x3
   }

   root = x3;
   return root;              //root of the equation
}

main() {
   double a, b, res;
   a = 0.5;
   b = 0.75;
   res = secant(a, b);
   cout << "The root is: " << res;
}

Đầu ra

The root is: -1.74166