Đồ thị được kết nối mạnh mẽ

Trong một đồ thị có hướng được cho là có liên kết chặt chẽ, khi có một đường đi giữa mỗi cặp đỉnh trong một thành phần.

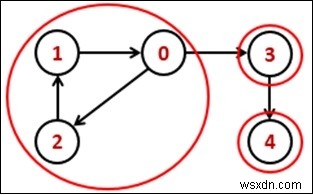
Để giải thuật toán này, trước hết, thuật toán DFS được sử dụng để lấy thời gian kết thúc của mỗi đỉnh, bây giờ tìm thời gian kết thúc của đồ thị chuyển vị, sau đó các đỉnh được sắp xếp theo thứ tự giảm dần theo cách sắp xếp tôpô.

Đầu vào và Đầu ra

Input:
Adjacency matrix of the graph.
0 0 1 1 0
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
0 0 0 0 0

Output:
Following are strongly connected components in given graph:
0 1 2
3
4

Thuật toán

đi ngang (biểu đồ, bắt đầu, đã truy cập)

Đầu vào: Biểu đồ sẽ được duyệt qua, đỉnh bắt đầu và cờ của các nút đã truy cập.

Đầu ra: Đi qua từng nút trong kỹ thuật DFS và các nút hiển thị.

Begin
   mark start as visited
   for all vertices v connected with start, do
      if v is not visited, then
         traverse(graph, v, visited)
   done
End

topoSort (u, đã truy cập, ngăn xếp)

Đầu vào - Nút bắt đầu, cờ cho các đỉnh đã thăm, ngăn xếp.

Đầu ra - Điền vào ngăn xếp trong khi sắp xếp biểu đồ.

Begin
   mark u as visited
   for all node v, connected with u, do
      if v is not visited, then
         topoSort(v, visited, stack)
   done
   push u into the stack
End

getStrongConComponents (đồ thị)

Đầu vào: Biểu đồ đã cho.

Đầu ra - Tất cả các thành phần được kết nối mạnh mẽ.

Begin
   initially all nodes are unvisited
   for all vertex i in the graph, do
      if i is not visited, then
         topoSort(i, vis, stack)
   done

   make all nodes unvisited again
   transGraph := transpose of given graph

   while stack is not empty, do
      pop node from stack and take into v
      if v is not visited, then
         traverse(transGraph, v, visited)
   done
End

Ví dụ

#include <iostream>
#include <stack>
#define NODE 5
using namespace std;

int graph[NODE][NODE] = {
   {0, 0, 1, 1, 0},
   {1, 0, 0, 0, 0},
   {0, 1, 0, 0, 0},
   {0, 0, 0, 0, 1},
   {0, 0, 0, 0, 0}
};
                               
int transGraph[NODE][NODE];

void transpose() {    //transpose the graph and store to transGraph
   for(int i = 0; i<NODE; i++)
      for(int j = 0; j<NODE; j++)
         transGraph[i][j] = graph[j][i];
}    
         
void traverse(int g[NODE][NODE], int u, bool visited[]) {
   visited[u] = true;    //mark v as visited
   cout << u << " ";

   for(int v = 0; v<NODE; v++) {
      if(g[u][v]) {
         if(!visited[v])
            traverse(g, v, visited);
      }
   }
}  
                                               
void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;    //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {    //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }

   stk.push(u);    //push starting vertex into the stack
}

void getStrongConComponents() {
   stack<int> stk;
   bool vis[NODE];

   for(int i = 0; i<NODE; i++)
      vis[i] = false;    //initially all nodes are unvisited
   
   for(int i = 0; i<NODE; i++)
      if(!vis[i])    //when node is not visited
         topoSort(i, vis, stk);
   
   for(int i = 0; i<NODE; i++)
      vis[i] = false;    //make all nodes are unvisited for traversal  
   transpose();    //make reversed graph
   
   while(!stk.empty()) {    //when stack contains element, process in topological order
      int v = stk.top(); stk.pop();
      if(!vis[v]) {
         traverse(transGraph, v, vis);
         cout << endl;
      }
   }
}

int main() {
   cout << "Following are strongly connected components in given graph: "<<endl;
   getStrongConComponents();
}

Đầu ra

Following are strongly connected components in given graph:
0 1 2
3
4