Giả sử chúng ta có một đồ thị. Chúng ta phải kiểm tra xem đồ thị có được kết nối mạnh mẽ hay không bằng cách sử dụng thuật toán Kosaraju. Một đồ thị được cho là có tính liên kết chặt chẽ, nếu bất kỳ hai đỉnh nào có đường đi giữa chúng thì đồ thị đó được kết nối với nhau. Biểu đồ vô hướng là biểu đồ được kết nối chặt chẽ.
Một số đồ thị vô hướng có thể được kết nối nhưng không được kết nối mạnh mẽ. Đây là một ví dụ về biểu đồ được kết nối mạnh mẽ.
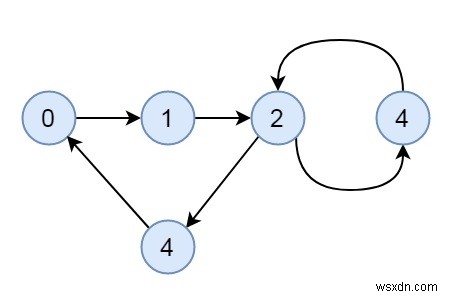
Đây là một ví dụ về biểu đồ được kết nối nhưng không được kết nối mạnh mẽ.
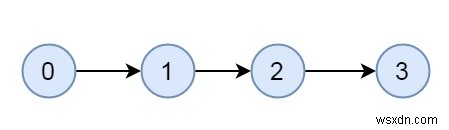
Ở đây chúng ta sẽ thấy, làm thế nào để kiểm tra một biểu đồ được kết nối mạnh mẽ hay không bằng cách sử dụng các bước sau của thuật toán Kosaraju.
Các bước -
-
Đánh dấu tất cả các nút là không được truy cập
-
Bắt đầu duyệt DFS từ bất kỳ đỉnh u tùy ý nào. Nếu DFS không truy cập được tất cả các nút, thì trả về false.
-
Đảo ngược tất cả các cạnh của biểu đồ
-
Đặt tất cả các đỉnh là các nút không được truy cập lại
-
Bắt đầu duyệt DFS từ đỉnh u đó. Nếu DFS không truy cập được tất cả các nút, thì trả về false. nếu không thì đúng.
Ví dụ
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph {
int V;
list<int> *adj;
void dfs(int v, bool visited[]);
public:
Graph(int V) {
this->V = V;
adj = new list<int>[V];
}
~Graph() {
delete [] adj;
}
void addEdge(int v, int w);
bool isStronglyConnected();
Graph reverseArc();
};
void Graph::dfs(int v, bool visited[]) {
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
dfs(*i, visited);
}
Graph Graph::reverseArc() {
Graph graph(V);
for (int v = 0; v < V; v++) {
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
graph.adj[*i].push_back(v);
}
return graph;
}
void Graph::addEdge(int u, int v) {
adj[u].push_back(v);
}
bool Graph::isStronglyConnected() {
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
Graph graph = reverseArc();
for(int i = 0; i < V; i++)
visited[i] = false;
graph.dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
int main() {
Graph graph(5);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
graph.addEdge(3, 0);
graph.addEdge(2, 4);
graph.addEdge(4, 2);
graph.isStronglyConnected()? cout << "This is strongly connected" : cout << "This is not strongly connected";
} Đầu ra
This is strongly connected
