Để kiểm tra khả năng kết nối của một biểu đồ, chúng tôi sẽ cố gắng duyệt qua tất cả các nút bằng bất kỳ thuật toán duyệt nào. Sau khi hoàn thành việc truyền tải, nếu có bất kỳ nút nào không được truy cập, thì biểu đồ không được kết nối.
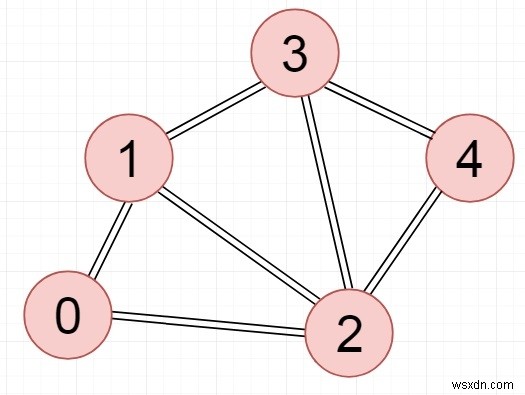
Đối với biểu đồ vô hướng, chúng tôi sẽ chọn một nút và đi qua từ đó.
Trong trường hợp này, thuật toán truyền tải là thuật toán truyền tải DFS đệ quy.
Đầu vào - Ma trận kề của đồ thị
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
Đầu ra - Biểu đồ được kết nối.
Thuật toán
traverse (u, đã ghé thăm)
Đầu vào - Nút bắt đầu u và nút đã truy cập để đánh dấu nút nào được truy cập.
Đầu ra:Đi ngang qua tất cả các đỉnh được kết nối.
Begin
mark u as visited
for all vertex v, if it is adjacent with u, do
if v is not visited, then
traverse(v, visited)
done
End isConnected (đồ thị)
Đầu vào - Biểu đồ.
Đầu ra - Đúng nếu biểu đồ được kết nối.
Begin define visited array for all vertices u in the graph, do make all nodes unvisited traverse(u, visited) if any unvisited node is still remaining, then return false done return true End
Mã mẫu
#include<iostream>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 0, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 1, 1},
{0, 1, 1, 0, 1},
{0, 0, 1, 1, 0}};
void traverse(int u, bool visited[]) {
visited[u] = true; //mark v as visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(!visited[v])
traverse(v, visited);
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i<NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i<NODE; i++) {
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
int main() {
if(isConnected())
cout << "The Graph is connected.";
else
cout << "The Graph is not connected.";
} Đầu ra:
The Graph is connected.
