Giả sử chúng ta có một đồ thị liên thông; chúng ta phải kiểm tra xem đồ thị có phải là lưỡng phân hay không. Nếu có thể tô màu biểu đồ, hãy áp dụng hai màu sao cho các nút trong một tập hợp được tô cùng màu.
Vì vậy, nếu đầu vào giống như
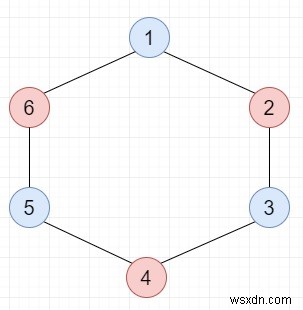
thì đầu ra sẽ là True
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một hàm insert_edge (), điều này sẽ lấy mảng cạnh là adj, u, v,
- chèn v vào cuối adj [u]
- chèn u vào cuối adj [v]
- Từ phương pháp chính, hãy làm như sau,
- đối với mỗi u trong adj [v], thực hiện
- nếu được truy cập [u] giống với sai, thì -
- đã ghé thăm [u]:=true
- color [u]:=invert of color [v]
- nếu không phải is_bipartite_graph (adj, u, đã thăm, màu), thì -
- trả về false
- ngược lại khi màu [u] giống với màu [v] thì -
- trả về false
- nếu được truy cập [u] giống với sai, thì -
- trả về true
Ví dụ (C ++)
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
void insert_edge(vector<int> adj[], int u, int v){
adj[u].push_back(v);
adj[v].push_back(u);
}
bool is_bipartite_graph(vector<int> adj[], int v, vector<bool>& visited, vector<int>& color){
for (int u : adj[v]) {
if (visited[u] == false) {
visited[u] = true;
color[u] = !color[v];
if (!is_bipartite_graph(adj, u, visited, color))
return false;
}
else if (color[u] == color[v])
return false;
}
return true;
}
int main() {
int N = 6;
vector<int> adj_list[N + 1];
vector<bool> visited(N + 1);
vector<int> color(N + 1);
insert_edge(adj_list, 1, 2);
insert_edge(adj_list, 2, 3);
insert_edge(adj_list, 3, 4);
insert_edge(adj_list, 4, 5);
insert_edge(adj_list, 5, 6);
insert_edge(adj_list, 6, 1);
visited[1] = true;
color[1] = 0;
cout << (is_bipartite_graph(adj_list, 1, visited, color));
} Đầu vào
insert_edge(adj_list, 1, 2); insert_edge(adj_list, 2, 3); insert_edge(adj_list, 3, 4); insert_edge(adj_list, 4, 5); insert_edge(adj_list, 5, 6); insert_edge(adj_list, 6, 1);
Đầu ra
1
