Diện tích của một đa giác đều n cạnh với độ dài cạnh cho trước trong C ++

Trong bài toán tìm diện tích của một đa giác đều n cạnh với một cạnh cho trước, chúng ta sẽ suy ra công thức về diện tích của hình đó và lập một chương trình dựa trên đó. Nhưng trước đó, hãy ôn lại những điều cơ bản để hiểu chủ đề một cách dễ dàng.

Đa giác đều N cạnh là một đa giác có n cạnh trong đó tất cả các cạnh đều bằng nhau. Ví dụ:ngũ giác đều, lục giác đều, v.v.

Khu vực là đại diện định lượng về mức độ của bất kỳ hình hai chiều nào.

Để tìm diện tích của hình này, chúng ta cần tìm diện tích của các tam giác riêng lẻ trong hình và nhân nó với số cạnh của nó. Vì chúng ta được đưa ra về phía.

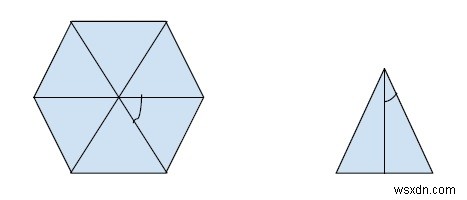
Bây giờ, từ hình trên, chúng ta có thể tạo công thức cho vùng.

Mỗi cạnh của đa giác đều có thể tạo ra một tam giác có cạnh a (cạnh của đa giác) và góc 180 / n (n là số cạnh của đa giác). Vì vậy, khu vực có thể được tìm thấy bằng cách sử dụng công thức,

Diện tích tam giác =½ * b * h

Bây giờ, h =a * tan (180 / n)

So , area = ½ * a * a / 2 * tan(180/n)
= a * a / (4 * tan(180/n))

Sử dụng công thức này cho một tam giác riêng lẻ của đa giác, chúng ta có thể tạo diện tích của cả đa giác,

Diện tích đa giác đều n cạnh =n * (a * a / (4 * tan (180 / n)))

Thuật toán

Step 1 : calculate the value of angle using (180 / n)
Step 2 : Calculate the area of regular polygon using n * (a * a / (4 * tan(180 /n))) .
Step 3 : Print the area of polygon.

Ví dụ

#include<iostream>
#include<math.h>
using namespace std;
int main(){
   float a = 12, n = 9;
   float area=(a * a * n) / (4 * tan((180 / n) * 3.14159 / 180));
   cout<<"The area of "<<n<<" sided regular polygon of side "<<a<<" is "<<area;
   return 0;
}

Đầu ra

The area of 9 sided regular polygon of side 12 is 890.183