Chúng tôi được cung cấp một mảng chiều cao của các bức tường của thùng chứa. Mục đích là tìm thùng chứa có thể chứa lượng nước tối đa. Vì chiều cao của các bức tường là các phần tử của một mảng, nên khoảng cách giữa chúng được coi là chiều rộng giữa hai bức tường. Ví dụ các bức tường của chiều cao Arr [i] và Arr [j] có chiều rộng j-i giữa chúng (0 <=i
Vì vậy, chiều cao của nước sẽ lên đến chiều cao nhỏ hơn, nếu Arr [i]
Chúng ta phải tìm ra diện tích tối đa như vậy.
Như trong hình, chiều cao tường 5,1,2,3 và chiều rộng tối đa giữa các bức tường là
Vùng chứa tối đa sẽ có nước tối đa, diện tích =20, tường Arr [0] và Arr [4]
Thùng chứa diện tích tối đa sẽ có nước tối đa, diện tích =16, tường Arr [0] và Arr [4]
Các bức tường của mảng số nguyên [] chứa chiều cao của các bức tường.
Hàm mostwater (int A [], int len) nhận mảng chiều cao và số không. của các phần tử trong đó và trả về diện tích của thùng chứa có hầu hết nước vì chỉ có chiều cao và chiều rộng.
Chúng tôi lấy hai chỉ mục r =len-1 và l =0 để bắt đầu duyệt mảng từ cả hai đầu.
Diện tích số nguyên và vùng tối đa được sử dụng để lưu trữ diện tích của vùng chứa hiện tại và vùng chứa tối đa được tìm thấy cho đến nay tương ứng. Ban đầu là 0
int minwall, lwall, rwall lưu trữ chiều cao của tường bên trái (A [l]), tường bên phải (A [r]) và chiều cao tối thiểu của tường và rwall;
Trong khi (l
Chiều rộng giữa hai bức tường là hiệu số của các chỉ mục (r-l)
Tính diện tích nước / thùng chứa dưới dạng tường nhỏ * (r-l) và diện tích cập nhật.
Làm điều này cho tất cả các bức tường, nếu diện tích hiện tại là tối đa cho đến nay, hãy cập nhật maxarea.
Cuối cùng thì maxarea sẽ có diện tích thùng chứa mong muốn với hầu hết nước. Đầu vào
Arr[]= { 5,1,2,3,5 } Đầu ra
Maximum water area : 20
Giải thích
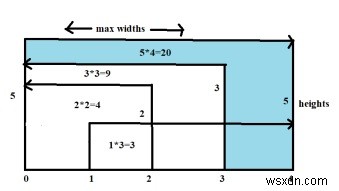
Arr[0] and Arr[4] width=4, area = Arr[0]<=Arr[4] → 5*4=20
Arr[1] and Arr[4] width=3, area = Arr[1]<=Arr[4] → 1*4=4
Arr[2] and Arr[0] or Arr[4] width=4, area = Arr[0]<=Arr[0] → 2*2=4
Arr3] and Arr[0] width=3, area = Arr[0]<=Arr[0] → 3*3=9
Arr[4] and Arr[0] width=4, area = Arr[0]<=Arr[4] → 5*4=20
Đầu vào
Arr[]= { 1, 5, 4, 3, 2, 4 } Đầu ra
Maximum water area : 16
Giải thích
Arr[0] and Arr[5] width=5, area = Arr[0]<=Arr[5] → 1*5= 5
Arr[1] and Arr[5] width=4, area = Arr[1]<=Arr[5] → 4*4=16
Arr[2] and Arr[5] width=3, area = Arr[2]<=Arr[5] → 3*4=12
Arr[3] and Arr[1] width=2, area = Arr[3]<=Arr[1] → 3*2=6
Arr[4] and Arr[1] width=3, area = Arr[1]<=Arr[4] → 2*3=6
Arr[5] and Arr[1] width=4, area = Arr[1]<=Arr[4] → 4*4=16
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau
Ví dụ
#include<iostream>
using namespace std;
int mostwater(int A[], int len){
int r=len-1; //index of right wall of container
int l=0; //index of left wall of container
int area=0,maxarea=0;
int minwall,lwall,rwall;
// int area = 0;
while (l < r){
// Calculating the max area
lwall = A[l]; //height of left wall of container
rwall =A[r]; //height of right wall of container
minwall=lwall<=rwall?lwall:rwall; //min. of two walls is height of water
area=minwall*(r-l); // area is min wall* widht(r-l)
maxarea=area>=maxarea?area:maxarea;
if (l < r)
l += 1;
else
r -= 1;
}
return maxarea;
}
int main(){
int walls[] = {1, 5, 4, 3, 2, 4};
int num = sizeof(walls) / sizeof(walls[0]);
cout << endl <<"Container with Most water has area:"<< mostwater(walls,num);
} Đầu ra
Container with Most water has area:16
