Giả sử chúng ta có một danh sách các hình chữ nhật (theo trục). Ở đây mỗi hình chữ nhật [i] ={x1, y1, x2, y2}, trong đó (x1, y1) là điểm của góc dưới bên trái và (x2, y2) là điểm của góc trên bên phải của hình chữ nhật thứ i.
Chúng ta phải tìm tổng diện tích được bao phủ bởi tất cả các hình chữ nhật trong mặt phẳng. Câu trả lời có thể là rất, vì vậy chúng ta có thể sử dụng modulo 10 ^ 9 + 7.
Vì vậy, nếu đầu vào giống như
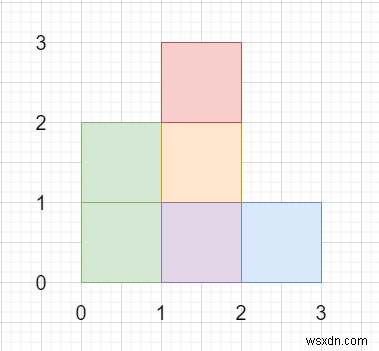
thì đầu ra sẽ là 6.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
m =10 ^ 9 + 7
-
Xác định một hàm add (), điều này sẽ lấy a, b,
-
return ((a mod m) + (b mod m) mod m)
-
Xác định một chức năng nén, điều này sẽ lấy ma trận 2d v
-
Xác định tạm thời mảng
-
để khởi tạo i:=0, khi i
-
chèn v [i, 0] vào cuối tạm thời
-
insert v [i, 2] vào cuối temp
-
-
sắp xếp tạm thời mảng
-
Xác định một bản đồ, ret
-
idx:=0
-
để khởi tạo i:=0, khi i
-
nếu temp [i] không phải là thành viên của ret, thì -
-
ret [temp [i]]:=idx
-
(tăng idx lên 1)
-
-
-
trả lại ret
-
Từ phương thức chính, hãy làm như sau -
-
Xác định một mảng xv
-
chèn {0} vào cuối xv
-
để khởi tạo i:=0, khi i
-
chèn v [i, 0] vào cuối xv
-
chèn v [i, 2] vào cuối xv
-
-
sắp xếp mảng xv
-
uniItr =phần tử đầu tiên của danh sách với các phần tử duy nhất của xv
-
xóa uniItr, khỏi xv
-
Xác định một chỉ mục bản đồ
-
idx:=0
-
để khởi tạo i:=0, khi i
-
index [xv [i]]:=i
-
-
Xác định số lượng mảng có kích thước giống như kích thước chỉ mục
-
Xác định một mảng 2D x
-
để khởi tạo i:=0, khi i
-
x1:=v [i, 0], y1:=v [i, 1]
-
x2:=v [i, 2], y2:=v [i, 3]
-
chèn {y1, x1, x2, 1} vào cuối x
-
chèn {y2, x1, x2, -1} vào cuối x
-
-
sắp xếp mảng x
-
ret:=0
-
sum:=0, currentY:=0
-
để khởi tạo i:=0, khi i
-
y:=x [i, 0]
-
x1:=x [i, 1], x2:=x [i, 2]
-
sig:=x [i, 3]
-
ret:=add (ret, (y - currentY) * sum)
-
hiện tạiY:=y
-
để khởi tạo i:=index [x1], khi tôi
-
count [i]:=count [i] + sig
-
-
tổng:=0
-
để khởi tạo i:=0, khi tôi
-
nếu đếm [i]> 0 thì
-
sum:=sum + (xv [i + 1] - xv [i])
-
-
-
-
trả lại bản sửa đổi m
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
const int m = 1e9 + 7;
class Solution {
public:
lli add(lli a, lli b){
return ((a % m) + (b % m) % m);
}
map<int, int> compress(vector<vector<int> >& v){
vector<int> temp;
for (int i = 0; i < v.size(); i++) {
temp.push_back(v[i][0]);
temp.push_back(v[i][2]);
}
sort(temp.begin(), temp.end());
map<int, int> ret;
int idx = 0;
for (int i = 0; i < temp.size(); i++) {
if (!ret.count(temp[i])) {
ret[temp[i]] = idx;
idx++;
}
}
return ret;
}
int rectangleArea(vector<vector<int> >& v){
vector<int> xv;
xv.push_back({ 0 });
for (int i = 0; i < v.size(); i++) {
xv.push_back(v[i][0]);
xv.push_back(v[i][2]);
}
sort(xv.begin(), xv.end());
vector<int>::iterator uniItr = unique(xv.begin(), xv.end());
xv.erase(uniItr, xv.end());
map<int, int> index;
int idx = 0;
for (int i = 0; i < xv.size(); i++) {
index[xv[i]] = i;
}
vector<int> count(index.size());
vector<vector<int> > x;
int x1, x2, y1, y2;
for (int i = 0; i < v.size(); i++) {
x1 = v[i][0];
y1 = v[i][1];
x2 = v[i][2];
y2 = v[i][3];
x.push_back({ y1, x1, x2, 1 });
x.push_back({ y2, x1, x2, -1 });
}
sort(x.begin(), x.end());
lli ret = 0;
lli sum = 0, currentY = 0;
for (int i = 0; i < x.size(); i++) {
lli y = x[i][0];
x1 = x[i][1];
x2 = x[i][2];
int sig = x[i][3];
ret = add(ret, (y - currentY) * sum);
currentY = y;
for (int i = index[x1]; i < index[x2]; i++) {
count[i] += sig;
}
sum = 0;
for (int i = 0; i < count.size(); i++) {
if (count[i] > 0) {
sum += (xv[i + 1] - xv[i]);
}
}
}
return ret % m;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,0,2,2},{1,0,2,3},{1,0,3,1}};
cout << (ob.rectangleArea(v));
} Đầu vào
{{0,0,2,2},{1,0,2,3},{1,0,3,1}} Đầu ra
6
