Giả sử chúng ta có một đường tròn được biểu diễn là (bán kính, xc, yc), ở đây (xc, yc) là tọa độ tâm của đường tròn. Chúng tôi cũng có một hình chữ nhật theo trục được biểu diễn là (x1, y1, x2, y2), trong đó (x1, y1) là tọa độ của góc dưới bên trái và (x2, y2) là tọa độ của góc trên bên phải góc của hình chữ nhật. Chúng ta phải kiểm tra xem hình tròn và hình chữ nhật có bị chồng lên nhau hay không.
Vì vậy, nếu đầu vào giống như
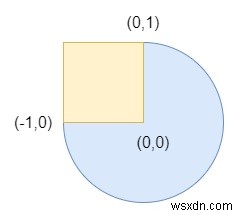
thì đầu ra sẽ là true.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Xác định một hàm eval (), điều này sẽ lấy a, b, c,
-
trả về tối đa là b và tối thiểu là a và c
-
Từ phương thức chính, thực hiện như sau -
-
cdx:=eval (cx, left, right), cdy:=eval (cy, bottom, top)
-
rwid:=right - left, rh:=top - bottom
-
dx:=cx - cdx, dy:=cy - cdy
-
disSq:=(dx * dx) + (dy * dy)
-
sqrRadius:=(r * r)
-
trả về true khi disSq <=sqrRadius, ngược lại là false
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int eval(int a, int b, int c){
return max(b, min(a, c));
}
bool checkOverlap(int r, int cx, int cy, int left, int bottom, int right, int top){
double cdx = eval(cx, left, right);
double cdy = eval(cy, bottom, top);
double rwid = right - left;
double rh = top - bottom;
double dx = cx - cdx;
double dy = cy - cdy;
double disSq = (dx * dx) + (dy * dy);
double sqrRadius = (r * r);
return (disSq <= sqrRadius);
}
};
main(){
Solution ob;
cout << (ob.checkOverlap(1, 0, 0, 1, -1, 3, 1));
} Đầu vào
1, 0, 0, 1, -1, 3, 1
Đầu ra
1
