Thùng chứa nhiều nước nhất bằng Python

Giả sử chúng ta có một bộ n số nguyên không âm a1, a2, ..., an, mỗi giá trị đại diện cho một điểm tại tọa độ (i, a [i]). n đường thẳng đứng có mặt sao cho hai điểm cuối của dòng i ở (i, a [i]) và (i, a [0]). Chúng ta phải tìm hai dòng, cùng với trục x tạo thành một thùng chứa, vì vậy mục tiêu của chúng tôi là tìm hai cột mà lượng nước là tối đa. Vì vậy, nếu mảng giống như [1,8,6,2,5,4,8,3,7], thì nó sẽ là

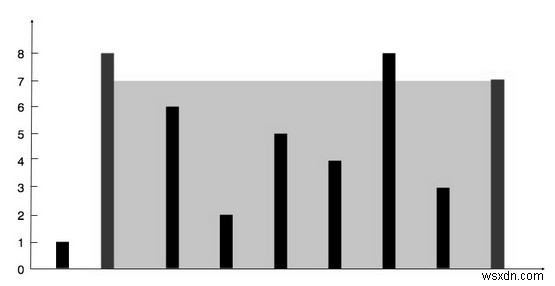
Trong phần bóng mờ, chiều cao là 7 và có 7 phần, vì vậy tổng diện tích thực tế là 7 * 7 =49. Đây là kết quả.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau

• low:=0, high:=length of arr - 1, ans:=0
• trong khi thấp
• if arr [low]
• nếu không thì min_h:=height [high] và min_ind:=high
• ans:=tối đa (cao - thấp) * min_h và ans
• nếu thấp + 1 =min_ind + 1, sau đó tăng thấp 1, nếu không giảm cao 1

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

class Solution(object):
   def maxArea(self, height):
      low = 0
      high = len(height) - 1
      ans = 0
      while low < high:
         if height[low]<height[high]:
            min_height = height[low]
            min_height_index = low
         else:
            min_height = height[high]
            min_height_index = high
         ans = max(((high - low) ) * min_height,ans)
         if low+1==min_height_index+1:
            low+=1
         else:
            high-=1
      return ans
ob1 = Solution()
print(ob1.maxArea([1,8,6,2,5,4,8,3,7]))

Đầu vào

[1,8,6,2,5,4,8,3,7]

Đầu ra

49