Trong bài toán này, chúng ta đưa ra một mảng arr gồm N số trong đó arr [i] đại diện cho nút thứ (i + 1). Ngoài ra, có M cặp cạnh trong đó u và v đại diện cho nút được nối bởi cạnh. Nhiệm vụ của chúng ta là tạo một chương trình để tìm tổng các phần tử tối thiểu trong tất cả các thành phần được kết nối của một đồ thị vô hướng. Nếu một nút không có kết nối với bất kỳ nút nào khác, hãy tính nó như một thành phần có một nút.
Hãy lấy một ví dụ để hiểu vấn đề,
Đầu vào
arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5 Đầu ra
8
Giải thích
Dưới đây là biểu đồ được mô tả ở trên -
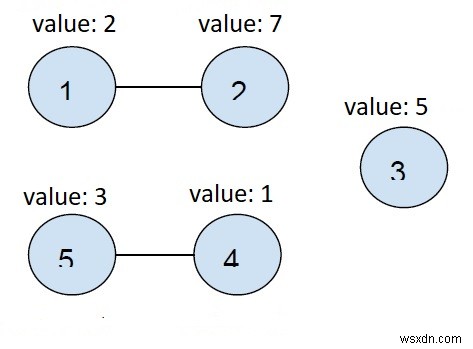
Chúng tôi có hai nút được kết nối và một nút duy nhất
Vì vậy, hãy tối thiểu hóa tất cả các thành phần được kết nối
Min (node1 và node2) =min (2, 7) =2
Min (node4 và node5) =min (1, 3) =1
Min (node3) =min (5) =5
Tổng =1 + 2 + 5 =8
Để giải quyết vấn đề này, chúng tôi sẽ tìm tất cả các nút được kết nối của biểu đồ vô hướng bằng cách sử dụng bất kỳ kỹ thuật truyền tải nào (BFS hoặc DFS) và sau đó tạo một mảng đã truy cập cho tất cả các nút được truy cập mà không có lần truy cập kép nào không có ở đó. Khi truy cập các nút được kết nối được kết nối trực tiếp hoặc gián tiếp, chúng tôi sẽ tìm thấy mức tối thiểu của tất cả các kết nối. Và thêm giá trị nhỏ nhất này của biến thesum. Sau khi chúng tôi đã truy cập tất cả các nút, chúng tôi sẽ in ra tổng.
Ví dụ
Chương trình minh họa hoạt động của giải pháp của chúng tôi,
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
minimum = min(minimum, arr[node]);
visited[node] = true;
for (int i : graph[node]) {
if (!visited[i])
dfs(i, arr, minimum);
}
}
void createEdge(int u, int v){
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
int sum = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int minimum = arr[i];
dfs(i, arr, minimum);
sum += minimum;
}
}
return sum;
}
int main(){
int arr[] = {2, 7, 5, 1, 3};
createEdge(1, 2);
createEdge(4, 5);
int n = sizeof(arr) / sizeof(arr[0]);
cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
cout<<minSum(arr, n);
return 0;
} Đầu ra
The sum of minimum elements in all connected components of an undirected graph is 8
