In tất cả các chu kỳ trong một đồ thị vô hướng trong C ++

Trong bài toán này, chúng ta được cung cấp một đồ thị vô hướng và chúng ta phải in tất cả các chu trình được hình thành trong đồ thị.

Biểu đồ vô hướng là một đồ thị được kết nối với nhau. Tất cả các cạnh của đồ thị một chiều là hai chiều. Nó còn được gọi là mạng vô hướng.

Chu kỳ trong cấu trúc dữ liệu đồ thị là một đồ thị trong đó tất cả các đỉnh tạo thành một chu trình.

Hãy xem một ví dụ để hiểu rõ vấn đề hơn -

Biểu đồ-

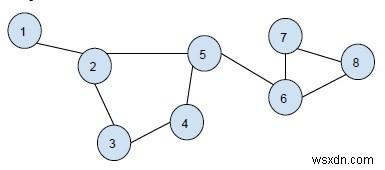
Đầu ra-

Cycle 1: 2 3 4 5
Cycle 2: 6 7 8

Đối với điều này, chúng tôi sẽ sử dụng một vài thuộc tính của biểu đồ. Bạn cần sử dụng phương pháp tô màu đồ thị và tô màu tất cả các đỉnh xuất hiện trong đồ thị tuần hoàn. Ngoài ra, nếu một đỉnh được thăm một phần, nó sẽ tạo ra một đồ thị tuần hoàn. Vì vậy, chúng tôi sẽ tô màu cho đỉnh này và tất cả các đỉnh tiếp theo cho đến khi đạt được cùng một lần nữa.

THUẬT TOÁN

Step 1: call DFS traversal for the graph which can color the vertices.
Step 2: If a partially visited vertex is found, backtrack till the vertex is
reached again and mark all vertices in the path with a counter which is cycle number.
Step 3: After completion of traversal, iterate for cyclic edge and push them
into a separate adjacency list.
Step 4: Print the cycles number wise from the adjacency list.

Ví dụ

#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
vector<int> graph[N];
vector<int> cycles[N];
void DFSCycle(int u, int p, int color[], int mark[], int par[], int&amp; cyclenumber){
   if (color[u] == 2) {
      return;
   }
   if (color[u] == 1) {
      cyclenumber++;
      int cur = p;
      mark[cur] = cyclenumber;
      while (cur != u) {
         cur = par[cur];
         mark[cur] = cyclenumber;
      }
      return;
   }
   par[u] = p;
   color[u] = 1;
   for (int v : graph[u]) {
      if (v == par[u]) {
         continue;
      }
      DFSCycle(v, u, color, mark, par, cyclenumber);
   }
   color[u] = 2;
}
void insert(int u, int v){
   graph[u].push_back(v);
   graph[v].push_back(u);
}
void printCycles(int edges, int mark[], int&amp; cyclenumber){
   for (int i = 1; i <= edges; i++) {
      if (mark[i] != 0)
         cycles[mark[i]].push_back(i);
   }
   for (int i = 1; i <= cyclenumber; i++) {
      cout << "Cycle " << i << ": ";
      for (int x : cycles[i])
         cout << x << " ";
      cout << endl;
   }
}
int main(){
   insert(1, 2);
   insert(2, 3);
   insert(3, 4);
   insert(4, 5);
   insert(5, 2);
   insert(5, 6);
   insert(6, 7);
   insert(7, 8);
   insert(6, 8);
   int color[N];
   int par[N];
   int mark[N];
   int cyclenumber = 0;
   cout<<"Cycles in the Graph are :\n";
   int edges = 13;
   DFSCycle(1, 0, color, mark, par, cyclenumber);
   printCycles(edges, mark, cyclenumber);
}

Đầu ra

Các chu kỳ trong Biểu đồ là -

Cycle 1: 2 3 4 5
Cycle 2: 6 7 8