Chúng tôi được cung cấp một cấu trúc dữ liệu cây với số nút ‘n’. Cây đã cho sẽ có một nút gốc và các nút con tương ứng có thể là bất kỳ số nào và cây con tiếp theo có thể có bất kỳ số lượng nút con nào. Nhiệm vụ là tìm số lần lặp tối thiểu mà một nút gốc của cây yêu cầu để truyền thông tin đến tất cả các nút trong cây. Tại một thời điểm, một nút có thể chuyển thông tin cho một trong các nút con của nó và xa hơn nữa, một trong các nút con của nó có thể chuyển thông tin cho một trong các nút con của nó và trong khi đó nút gốc có thể chuyển thông tin cho một nút con khác.
Hãy cho chúng tôi xem các tình huống đầu ra đầu vào khác nhau cho việc này -
Trong -
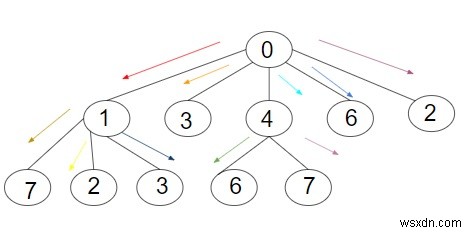
Hết - Số tối thiểu. số lần lặp để chuyển thông tin đến tất cả các nút trong cây là:5
Giải thích - Chúng ta được cung cấp một cây với tổng số 11 nút bao gồm gốc và tất cả các nút khác. Nút gốc của một cây nhất định là 0, trước tiên nó sẽ truyền dữ liệu cho nút 1 vì nó có nhiều nút con rồi đến các nút khác, sau đó nút gốc sẽ chuyển dữ liệu cho nút 4, sau đó nó sẽ truyền dữ liệu cho 3, sau đó nó sẽ chuyển dữ liệu thành 6 và cuối cùng nó sẽ chuyển dữ liệu đến 2. Vì vậy, tổng số lần lặp được yêu cầu là 5.
Trong -
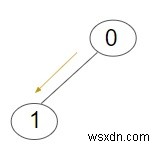
Hết - Số tối thiểu. số lần lặp để chuyển thông tin đến tất cả các nút trong cây là:1
Giải thích - :Chúng ta được cho một cây với tổng số 2 nút bao gồm gốc và tất cả các nút khác. Vì chỉ có một nút con của nút gốc trong một cây nhất định nên số lần lặp tối thiểu cần thiết sẽ là 1.
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau -
-
Tạo một lớp để xây dựng cây và thêm các nút làm thành viên dữ liệu của nó và tạo một con trỏ danh sách dưới dạng List_children và khai báo một phương thức private là void Iteration (int vertices, int arr []). Khai báo một phương thức khởi tạo được tham số hóa là Tree (int node), void insert_node (int a, int b), int Min_Iteration () và static int check (const void * a_1, const void * b_1).
-
Gọi một phương thức khởi tạo được tham số hóa bên ngoài là Tree ::Tree (int node)
-
Đặt this-> các nút thành các nút.
-
Đặt List_children thành danh sách mới [các nút]
-
-
Gọi một phương thức lớp là void Tree ::insert_node (int a, int b)
-
Đặt List_children [a] thành push_back (b)
-
-
Gọi một phương thức lớp là void Tree ::Iteration (int vertices, int arr [])
-
Đặt arr [vertices] thành List_children [vertices] .size ()
-
Đặt * ptr thành new int [arr [vertices]]
-
Đặt nhiệt độ thành 0 và nhiệt độ_2 thành 0
-
Khai báo một trình lặp dưới dạng danh sách ::trình lặp nó
-
Bắt đầu vòng lặp FOR từ nó đến List_children [đỉnh] .begin () cho đến khi nó không bằng List_children [đỉnh] .end () và tăng trước nó. Bên trong vòng lặp, thiết lập Iteration (* it, arr) và đặt ptr [temp ++] thành arr [* it]
-
Gọi qsort (ptr, arr [vertices], sizeof (int), check) để sắp xếp nhanh
-
Bắt đầu Vòng lặp FOR tạm thời đến 0 và nhiệt độ nhỏ hơn List_children [đỉnh] .size () và đăng nhiệt độ tăng dần. Bên trong vòng lặp, đặt temp_2 thành ptr [temp] + temp + 1 và arr [đỉnh] thành max (arr [đỉnh], temp_2) và xóa [] ptr
-
-
Gọi một phương thức lớp là int Tree ::Min_Iteration ()
-
Khai báo một con trỏ là int * ptr =new int [node]
-
Khai báo một biến là int temp =-1
-
Bắt đầu vòng lặp FOR từ i đến 0 cho đến khi i
-
Gọi Lặp lại (0, ptr) và đặt nhiệt độ thành ptr [0] và xóa [] ptr
-
trở lại nhiệt độ
-
-
Gọi một phương thức lớp là int Tree ::check (const void * a_1, const void * b_1)
-
Khai báo một biến dưới dạng kết quả int thành (* (int *) b_1 - * (int *) a_1)
-
trả về kết quả
-
-
Trong hàm main ()
-
Tạo một đối tượng cây bằng cách sử dụng một hàm tạo được tham số hóa.
-
Sau đó, sử dụng đối tượng của lớp cây, gọi phương thức insert_node () để chèn dữ liệu nút vào cây
-
Gọi phương thức Min_Iteration () để tính số lần lặp tối thiểu để chuyển thông tin đến tất cả các nút trong cây
-
Ví dụ
#include<bits/stdc++.h>
using namespace std;
class Tree
{
int nodes;
list<int> *List_children;
void Iteration(int vertices, int arr[]);
public:
//constructor of a class
Tree(int nodes);
//method to insert a node in a tree
void insert_node(int a, int b);
//method to calculate the minimum iterations
int Min_Iteration();
static int check(const void *a_1, const void *b_1);
};
Tree::Tree(int nodes)
{
this->nodes = nodes;
List_children = new list<int>[nodes];
}
void Tree::insert_node(int a, int b)
{
List_children[a].push_back(b);
}
void Tree::Iteration(int vertices, int arr[])
{
arr[vertices] = List_children[vertices].size();
int *ptr = new int[arr[vertices]];
int temp = 0;
int temp_2 = 0;
list<int>::iterator it;
for(it = List_children[vertices].begin(); it!= List_children[vertices].end(); ++it)
{
Iteration(*it, arr);
ptr[temp++] = arr[*it];
}
qsort(ptr, arr[vertices], sizeof(int), check);
for(temp = 0; temp < List_children[vertices].size(); temp++)
{
temp_2 = ptr[temp] + temp + 1;
arr[vertices] = max(arr[vertices], temp_2);
}
delete[] ptr;
}
int Tree::Min_Iteration()
{
int *ptr = new int[nodes];
int temp = -1;
for (int i = 0; i < nodes; i++)
{
ptr[i] = 0;
}
Iteration(0, ptr);
temp = ptr[0];
delete[] ptr;
return temp;
}
int Tree::check(const void * a_1, const void * b_1)
{
}
int main()
{
Tree T_1(8);
T_1.insert_node(0, 1);
T_1.insert_node(0, 3);
T_1.insert_node(0, 4);
T_1.insert_node(0, 6);
T_1.insert_node(0, 2);
T_1.insert_node(1, 7);
T_1.insert_node(1, 2);
T_1.insert_node(1, 3);
T_1.insert_node(4, 6);
T_1.insert_node(4, 7);
cout<<"Minimum no. of iterations to pass information to all nodes in the tree are:"<<T_1.Min_Iteration();
Tree T_2(2);
T_2.insert_node(0, 1);
cout<<"\nMinimum no. of iterations to pass information to all nodes in the tree are:" <<T_1.Min_Iteration();
return 0;
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra Kết quả sau
Minimum no. of iterations to pass information to all nodes in the tree are: 8 Minimum no. of iterations to pass information to all nodes in the tree are: 8
