Tìm đỉnh, tiêu điểm và ma trận trực tiếp của một parabol trong chương trình Python

Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu lệnh vấn đề được đưa ra bên dưới -

Tuyên bố vấn đề

Dạng chuẩn của phương trình parabol là y =ax ^ ² + bx + c. Nhập các giá trị của a, b và c, nhiệm vụ của chúng ta là tìm tọa độ của đỉnh, tiêu điểm và phương trình của ma trận.

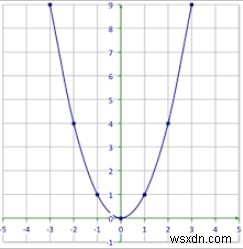
Đỉnh của một parabol là tọa độ mà từ đó nó chuyển hướng mạnh nhất trong khi y =a là đường thẳng được sử dụng để tạo ra đường cong.

Ma trận trực tiếp một đường cố định được sử dụng để mô tả một đường cong hoặc bề mặt.

Bây giờ chúng ta hãy xem việc triển khai -

Ví dụ

def findparabola(a, b, c):
   print ("Vertex: (" , (-b / (2 * a)) ,
", ",(((4 * a * c) - (b * b)) / (4 * a)) , ")" )

   print ("Focus: (" , (-b / (2 * a)) , ", ", (((4 * a * c) -(b * b) + 1) / (4 * a)) , ")" )

   print ("Directrix: y=", (int)(c - ((b * b) + 1) * 4 * a ))
# main()
a = 7
b = 5
c = 3

findparabola(a, b, c)

Đầu ra

Vertex: ( -0.35714285714285715 , 2.107142857142857 )
Focus: ( -0.35714285714285715 , 2.142857142857143 )
Directrix: y= -725

Tất cả các biến &hàm được khai báo trong phạm vi toàn cục như thể hiện trong hình bên dưới.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về cách tìm đỉnh, tiêu điểm và ma trận trực tiếp của một parabol