Chương trình kết nối một khu rừng bằng Python

Giả sử chúng ta có đồ thị dưới dạng danh sách kề. Đồ thị này thực sự là một tập hợp các cây rời rạc. Chúng ta phải thêm một số cạnh nhất định vào rừng để nó trở thành một cây duy nhất. Chúng ta phải trả lại khoảng cách tối thiểu có thể có của đường đi dài nhất giữa hai nút bất kỳ. Vì vậy, nếu đầu vào giống như

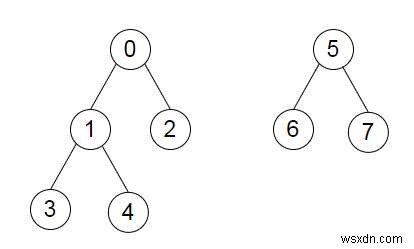
thì đầu ra sẽ là 4.

Chúng ta có thể thêm cạnh 0 -> 5. Khi đó, đường đi dài nhất có thể là bất kỳ trong 3 -> 1 -> 0 -> 5 -> 7 hoặc 4 -> 1 -> 0 -> 5 -> 7; và cả những con đường này với hướng bị đảo ngược. Vì vậy, chúng tôi trả lại khoảng cách 4.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

đã thấy:=một tập hợp mới
dic:=graph
Định nghĩa một cây hàmDepth (). Điều này sẽ sử dụng nút.
- ret:=0
- Định nghĩa một hàm dfs1 (). Điều này sẽ lấy nút, cha mẹ.
  - thêm một nút trong tập hợp đã thấy
  - best2:=một cấu trúc heap tối thiểu trống
  - đối với mỗi nxt trong dic [node], thực hiện
    - nếu nxt không giống với gốc, thì
      - push (dfs1 (nxt, node) + 1) vào best2
    - nếu len (best2)> 2, thì
      - bật lên từ đống (best2)
    - nếu best2 trống, thì
      - trả về 0
    - ret:=tối đa trong tổng số ret, tổng tất cả các phần tử của best2
    - trả về tối đa best2
  - dfs1 (nút, null)
  - trả lại ret
Từ phương thức chính, hãy làm như sau -
ret:=0, opt:=a new list, sing:=0
- đối với nút trong phạm vi từ 0 đến kích thước của biểu đồ, hãy thực hiện
  - nếu nút hiện diện trong saw, thì
    - chuyển sang lần lặp tiếp theo
  - res:=treeDepth (nút)
  - sing:=tối đa sing, res
  - chèn trần của (res / 2) vào cuối lựa chọn
- nếu kích thước của opt <=1, thì
  - hát trở lại
- mx:=tối đa lựa chọn
- đối với tôi trong phạm vi từ 0 đến kích thước tùy chọn, hãy thực hiện
  - nếu opt [i] giống với mx thì
    - opt [i]:=opt [i] - 1
    - đi ra từ vòng lặp
- đối với tôi trong phạm vi từ 0 đến kích thước tùy chọn, hãy thực hiện
  - opt [i]:=opt [i] + 1
- high2:=2 phần tử lớn nhất từ tùy chọn.
- trả về số tiền tối đa (high2) và hát

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

import heapq, math
class Solution:
   def solve(self, graph):
      seen = set()
      dic = graph
      def treeDepth(node):
         self.ret = 0
         def dfs1(node, parent):
            seen.add(node)
            best2 = []
            for nxt in dic[node]:
               if nxt != parent:
                  heapq.heappush(best2, dfs1(nxt, node) + 1)
                  if len(best2) > 2:
                     heapq.heappop(best2)
            if not best2:
               return 0
            self.ret = max(self.ret, sum(best2))
            return max(best2)
         dfs1(node, None)
         return self.ret
      ret = 0
      opt = []
      sing = 0
      for node in range(len(graph)):
         if node in seen:
            continue
         res = treeDepth(node)
         sing = max(sing, res)
         opt.append(int(math.ceil(res / 2)))
      if len(opt) <= 1:
         return sing
      mx = max(opt)
      for i in range(len(opt)):
         if opt[i] == mx:
            opt[i] −= 1
            break
         for i in range(len(opt)):
            opt[i] += 1
         high2 = heapq.nlargest(2, opt)
         return max(sum(high2), sing)
ob = Solution()
graph = [
   [1, 2],
   [0,3,4],
   [0],
   [1],
   [1],
   [6,7],
   [5],
   [5]
]
print(ob.solve(graph))

Đầu vào

graph = [
   [1, 2],
   [0,3,4],
   [0],
   [1],
   [1],
   [6,7],
   [5],
   [5]
]

Chương trình kết nối một khu rừng bằng Python

Ví dụ

Đầu vào

Đầu ra