Một vấn đề về đồ thị Peterson trong chương trình C?

Giả sử chúng ta có một đồ thị như dưới đây. Đồ thị đó là đồ thị Peterson. Các đỉnh được đánh số từ 0 đến 9. Mỗi đỉnh có một số chữ cái. Hãy xem xét một bước đi W, trong đồ thị đó, nơi sử dụng các đỉnh L. Một chuỗi S với các chữ cái L được thực hiện bởi bước đi W khi chuỗi ký tự trong W và S giống nhau. Chúng ta có thể thăm các đỉnh nhiều lần.

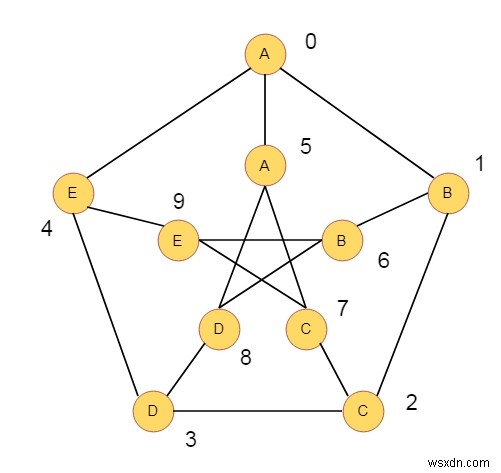
Ví dụ, một chuỗi S giống như “ABBECCD”, điều này được thực hiện bằng bước đi (0, 1, 6, 9, 7, 2, 3). Nhiệm vụ của chúng ta là tìm ra cuộc đi bộ như vậy, và nếu cuộc đi bộ đó có mặt, thì hãy tìm cách đi bộ đó về mặt từ vựng là ít nhất. Nếu không có bước đi nào ở đó, hãy trả về -1.

Thuật toán

petersonGraphWalk (S, v) -

begin
   res := starting vertex
   for each character c in S except the first one, do
      if there is an edge between v and c in outer graph, then      
         v := c
      else if there is an edge between v and c+5 in inner graph, then
         v := c + 5
      else
         return false
      end if
         put v into res
      done
   return true
end

Ví dụ

#include<iostream>
using namespace std;
bool adj_mat[10][10] = {{0, 1, 0, 0, 1, 1, 0, 0, 0, 0},
   {1, 0, 1, 0, 0, 0, 1, 0, 0, 0},
   {0, 1, 0, 1, 0, 0, 0, 1, 0, 0},
   {0, 0, 1, 0, 1, 0, 0, 0, 1, 0},
   {1, 0, 0, 1, 0, 0, 0, 0, 0, 1},
   {1, 0, 0, 0, 0, 0, 0, 1, 1, 0},
   {0, 1, 0, 0, 0, 0, 0, 0, 1, 1},
   {0, 0, 1, 0, 0, 1, 0, 0, 0, 1},
   {0, 0, 0, 1, 0, 1, 1, 0, 0, 0},
   {0, 0, 0, 0, 1, 0, 1, 1, 0, 0}
};
char S[100005];
char res[100005];
bool petersonGraphWalk(char* S, int v){
   res[0] = v + '0';
   for(int i = 1; S[i]; i++){
      //traverse the outer graph
      if(adj_mat[v][S[i] - 'A'] || adj_mat[S[i] - 'A'][v]){
         v = S[i] - 'A';
      }
      //then check the inner graph
      else if(adj_mat[v][S[i] - 'A' + 5] || adj_mat[S[i] - 'A' + 5][v]){
         v = S[i] - 'A' + 5;
      }else{
         return false;
      }
      res[i] = v + '0';
   }
   return true;
}
main() {
   char* str = "ABBECCD";
   if(petersonGraphWalk(str, str[0] - 'A') || petersonGraphWalk(str, str[0] - 'A' + 5)){
      cout << res;
   }else{
      cout << -1;
   }
}

Đầu ra

0169723