Chương trình Python cho vấn đề 0-1 Knapsack

Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu hỏi được đưa ra bên dưới.

Tuyên bố sự cố - Chúng ta được cho trước trọng lượng và giá trị của n món đồ, chúng ta cần cho những đồ vật này vào một túi có dung tích W đến dung tích lớn nhất là w. Chúng tôi cần mang theo số lượng tối đa các mặt hàng và trả lại giá trị của nó.

Bây giờ chúng ta hãy quan sát giải pháp trong việc triển khai bên dưới -

# Phương pháp tiếp cận vũ lực

Ví dụ

#Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   # initial conditions
   if n == 0 or W == 0 :
      return 0
   # If weight is higher than capacity then it is not included
   if (wt[n-1] > W):
      return knapSack(W, wt, val, n-1)
   # return either nth item being included or not
   else:
      return max(val[n-1] + knapSack(W-wt[n-1], wt, val, n-1),
         knapSack(W, wt, val, n-1))
# To test above function
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print (knapSack(W, wt, val, n))

Đầu ra

350

# phương pháp tiếp cận động lực học

Ví dụ

# a dynamic approach
# Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   K = [[0 for x in range(W + 1)] for x in range(n + 1)]
   #Table in bottom up manner
   for i in range(n + 1):
      for w in range(W + 1):
         if i == 0 or w == 0:
            K[i][w] = 0
         elif wt[i-1] <= w:
            K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
         else:
            K[i][w] = K[i-1][w]
   return K[n][W]
#Main
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print(knapSack(W, wt, val, n))

Đầu ra

350

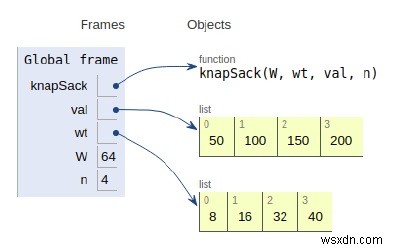
Tất cả các biến được khai báo trong phạm vi cục bộ và các tham chiếu của chúng được nhìn thấy trong hình trên.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về cách tạo Chương trình Python cho 0-1 Sự cố Knapsack