Thuật toán Bellman Ford là thuật toán lập trình động được sử dụng để tìm đường đi ngắn nhất của bất kỳ đỉnh nào được tính từ một đỉnh được coi là đỉnh xuất phát. thuật toán này tuân theo phương pháp lặp và liên tục cố gắng tìm đường đi ngắn nhất. Thuật toán Bellman Ford trên đồ thị có trọng số.
thuật toán này được Alphonso shimbel đề xuất vào năm 1955. Thuật toán đã được sửa đổi bởi Richard Bellman và Lester Ford vào năm 1956 và 1958, do thuật toán này được đặt tên là Thuật toán Bellman Ford . Thuật toán này cũng đã được sửa đổi bởi Eward F. Moore vào năm 1957, được đặt tên thành Thuật toán Bellman-Ford-Moore .
Thuật toán này tốt hơn vì nó có thể xử lý các cạnh có trọng số âm. Mặc dù thuật toán này chậm hơn so với thuật toán của Dijkstra, nhưng nó là một thuật toán tốt hơn vì nó xử lý nhiều loại biểu đồ linh hoạt hơn.
Thuật toán
Input : weighted graph and starting vertex Output : shortest distance between all vertices from the src. For negative weight cycle, the same will be returned as the weight cannot be calculated.
Thuật toán
Step 1 : This is the initialisation step, an array is created that stores the distance of all vertices from the initial vertex. The array say dist[] of size equal to the number of vertices in the graph. Step 2 : Calculate the shortest distance of vertex. Loop through step 3 for n-1 number of times ( n is the number of vertices of graph). Step 3 : Follow following steps for each edge i-j Step 3.1 : If dist[v] > dist[u] + weight[uv]. Then, dist[v] = dist[u] + weight[uv]. Step 4 : Check and flag if there is any negative cycle. If step 3.1 executes then there is a negative cycle.
Chu kỳ âm:Nếu tồn tại một đường đi ngắn hơn đường truyền cạnh thông thường, thì có một chu kỳ âm.
Ví dụ
Hãy cùng tìm hiểu thêm về thuật toán bằng cách giải một số vấn đề liên quan đến biểu đồ.
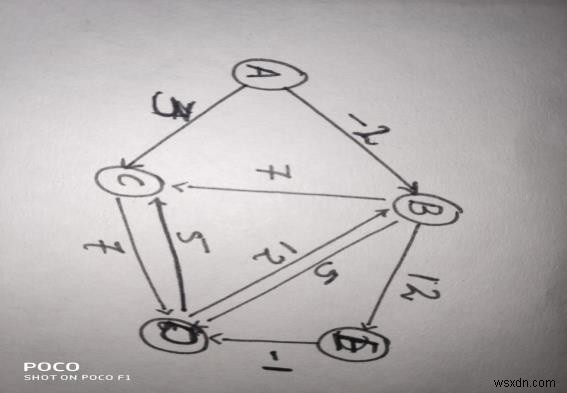
Bạn có thể thấy tất cả các đỉnh và cạnh của biểu đồ cùng với trọng số liên quan đến chúng.
Cho phép tìm khoảng cách ngắn nhất giữa đỉnh A và đỉnh E sử dụng Thuật toán Bellman-ford.
Đặt đỉnh nguồn (A) thành 0 0 và đặt khoảng cách còn lại thành vô cùng ∞.
A B C D E 0 ∞ ∞ ∞ ∞
Kiểm tra trọng lượng của cạnh A-B rồi đến A-C ,
Đối với A-B, chúng tôi chỉ có một con đường nhưng đối với A-C, chúng tôi có hai con đường có thể đi qua và chúng tôi sẽ kiểm tra con đường nào ngắn nhất.
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ - for (A-B) 0 -2 3 ∞ ∞ - for (A-C)
Đối với các đỉnh tiếp theo, chúng tôi sẽ tính toán và khoảng cách ngắn nhất cho đỉnh ban đầu.
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ 0 -2 3 3 10
Do đó, khoảng cách ngắn nhất sử dụng thuật toán là 10. Đi ngang qua đường dẫn A-B-E . Sử dụng điều này, chúng tôi cũng nhận thấy rằng có một chu kỳ tiêu cực.
Ví dụ
#include <bits/stdc++.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E) {
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
void BellmanFord(struct Graph* graph, int src) {
int V = graph->V;
int E = graph->E;
int dist[V];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
printf("Graph contains negative weight cycle");
return;
}
}
printf("Vertex :\t\t\t ");
for (int i = 0; i < V; ++i)
printf("%d \t", i);
printf("\nDistance From Source : ");
for (int i = 0; i < V; ++i)
printf("%d \t",dist[i]);
return;
}
int main() {
int V = 5;
int E = 8;
struct Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
BellmanFord(graph, 0);
return 0;
} Đầu ra
Vertex : 0 1 2 3 4 Distance From Source : 0 -1 2 -2 1
