Thuật toán Bellman – Ford cho những con đường ngắn nhất

Thuật toán Bellman-Ford được sử dụng để tìm khoảng cách tối thiểu từ đỉnh nguồn đến bất kỳ đỉnh nào khác. Sự khác biệt chính giữa thuật toán này với thuật toán Dijkstra là, trong thuật toán Dijkstra, chúng tôi không thể xử lý trọng số âm, nhưng ở đây chúng tôi có thể xử lý nó một cách dễ dàng.

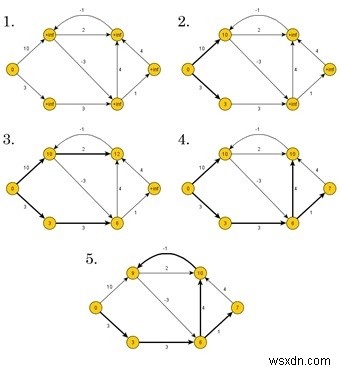
Thuật toán Bellman-Ford tìm khoảng cách theo cách từ dưới lên. Lúc đầu, nó tìm những khoảng cách chỉ có một cạnh trên đường đi. Sau đó, hãy tăng độ dài đường dẫn để tìm tất cả các giải pháp khả thi.

Đầu vào và Đầu ra

Input:
The cost matrix of the graph:
0  6  ∞ 7  ∞
∞  0  5 8 -4
∞ -2  0 ∞  ∞
∞  ∞ -3 0  9
2  ∞  7 ∞  0

Output:
Source Vertex: 2
Vert:   0   1   2   3   4
Dist:  -4  -2   0   3  -6
Pred:   4   2  -1   0   1
The graph has no negative edge cycle

Thuật toán

bellmanFord(dist, pred, source)

Đầu vào - Danh sách khoảng cách, danh sách tiền nhiệm và đỉnh nguồn.
Đầu ra - Đúng, khi một chu kỳ âm được tìm thấy.

Begin
   iCount := 1
   maxEdge := n * (n - 1) / 2     //n is number of vertices

   for all vertices v of the graph, do
      dist[v] := ∞
      pred[v] := ϕ
   done

   dist[source] := 0
   eCount := number of edges present in the graph
   create edge list named edgeList

   while iCount < n, do
      for i := 0 to eCount, do
         if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) pred[edgeList[i].v] := edgeList[i].u
      done
   done

   iCount := iCount + 1
   for all vertices i in the graph, do
      if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i),
         then return true
   done

   return false
End

Ví dụ

#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//Cost matrix of the graph (directed) vertex 5

int costMat[V][V] = {
   {0, 6, INF, 7, INF},
   {INF, 0, 5, 8, -4},
   {INF, -2, 0, INF, INF},
   {INF, INF, -3, 0, 9},
   {2, INF, 7, INF, 0}
};

typedef struct {
   int u, v, cost;
}edge;

int isDiagraph() {

   //check the graph is directed graph or not

   int i, j;
   for(i = 0; i<V; i++) {
      for(j = 0; j<V; j++) {
         if(costMat[i][j] != costMat[j][i]) {
            return 1;      //graph is directed
         }
      }
   }
   return 0;//graph is undirected
}

int makeEdgeList(edge *eList) {
   //create edgelist from the edges of graph
   int count = -1;
   if(isDiagraph()) {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<V; j++) {
            if(costMat[i][j] != 0 && costMat[i][j] != INF) {
               count++;         //edge find when graph is directed
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }else {
      for(int i = 0; i<V; i++) {
         for(int j = 0; j<i; j++) {
            if(costMat[i][j] != INF) {
               count++;         //edge find when graph is undirected
               eList[count].u = i; eList[count].v = j;
               eList[count].cost = costMat[i][j];
            }
         }
      }
   }
   return count+1;
}

int bellmanFord(int *dist, int *pred,int src) {
   int icount = 1, ecount, max = V*(V-1)/2;
   edge edgeList[max];

   for(int i = 0; i<V; i++) {
      dist[i] = INF;      //initialize with infinity
      pred[i] = -1;      //no predecessor found.
   }

   dist[src] = 0;//for starting vertex, distance is 0

   ecount = makeEdgeList(edgeList);       //edgeList formation

   while(icount < V) {       //number of iteration is (Vertex - 1)
      for(int i = 0; i<ecount; i++) {
         if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {      //relax edge and set predecessor
            dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
            pred[edgeList[i].v] = edgeList[i].u;
         }
      }
      icount++;
   }

   //test for negative cycle
   for(int i = 0; i<ecount; i++) {
      if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {
         return 1;    //indicates the graph has negative cycle
      }
   }

   return 0;     //no negative cycle
}

void display(int *dist, int *pred) {
   cout << "Vert: ";
   for(int i = 0; i<V; i++)
      cout <<setw(3) << i << " ";
   cout << endl;
   cout << "Dist: ";

   for(int i = 0; i<V; i++)
      cout << setw(3) << dist[i] << " ";
   cout << endl;
   cout << "Pred: ";

   for(int i = 0; i<V; i++)
      cout << setw(3) << pred[i] << " ";
   cout << endl;
}

int main() {
   int dist[V], pred[V], source, report;
   source = 2;
   report = bellmanFord(dist, pred, source);
   cout << "Source Vertex: " << source<<endl;
   display(dist, pred);

   if(report)
      cout << "The graph has a negative edge cycle" << endl;
   else
      cout << "The graph has no negative edge cycle" << endl;
}

Đầu ra

Source Vertex: 2
Vert:   0   1   2   3   4
Dist:  -4  -2   0   3  -6
Pred:   4   2  -1   0   1
The graph has no negative edge cycle