Có một đồ thị G (V, E) đã cho với biểu diễn danh sách kề của nó và một đỉnh nguồn cũng được cung cấp. Thuật toán Dijkstra để tìm đường đi ngắn nhất nhỏ nhất giữa đỉnh nguồn tới bất kỳ đỉnh nào khác của biểu đồ G.
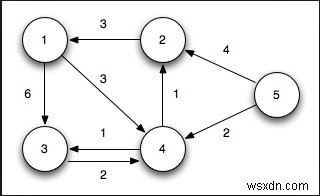
Để giải quyết vấn đề này, chúng tôi sẽ sử dụng hai danh sách. Một là lưu trữ các đỉnh đã được coi là cây đường đi ngắn nhất, và một là lưu trữ các đỉnh chưa được xem xét. Trong mỗi giai đoạn của thuật toán, chúng tôi tìm thấy đỉnh chưa được xét và có khoảng cách nhỏ nhất từ nguồn.
Một danh sách khác được sử dụng để giữ nút tiền nhiệm. Sử dụng nút tiền nhiệm, chúng ta có thể tìm thấy đường dẫn từ nguồn và đích.
Độ phức tạp của thuật toán đường đi ngắn nhất của Dijkstra là O (E log V) vì biểu đồ được biểu diễn bằng cách sử dụng danh sách kề . Ở đây E là số cạnh và V là Số đỉnh.
Đầu vào và Đầu ra
Input: The adjacency list of the graph with the cost of each edge.Output: 0 to 1, Cost: 3 Previous: 0 0 to 2, Cost: 5 Previous: 1 0 to 3, Cost: 4 Previous: 1 0 to 4, Cost: 6 Previous: 3 0 to 5, Cost: 7 Previous: 2 0 to 6, Cost: 7 Previous: 4
Thuật toán
dijkstraShortestPath(g : Graph, dist, prev, start : node)
Đầu vào - Biểu đồ g, danh sách dist để lưu trữ khoảng cách, danh sách trước cho các nút tiền nhiệm và đỉnh bắt đầu.
Đầu ra - Các đường đi ngắn nhất từ đầu đến tất cả các đỉnh khác.
Begin for all vertices u in (V - start) do dist[u] := ∞ prev[u] := φ done set dist[start] = 0 and prev[start] := φ for all node u in V do insert u into queue ‘Q’. done while Q is not empty do u := minimum element from Queue delete u from Q insert u into set S for each node v adjacent with node u do if dist[u]+cost(v) < dist[v] then dist[v] := dist[u]+cost(v) prev[v] := u done done End
Ví dụ
#include<iostream>
#include<set>
#include<list>
#include<algorithm>
using namespace std;
typedef struct nodes {
int dest;
int cost;
}node;
class Graph {
int n;
list<node> *adjList;
private:
void showList(int src, list<node> lt) {
list<node> :: iterator i;
node tempNode;
for(i = lt.begin(); i != lt.end(); i++) {
tempNode = *i;
cout << "(" << src << ")---("<<tempNode.dest << "|"<<tempNode.cost<<") ";
}
cout << endl;
}
public:
Graph() {
n = 0;
}
Graph(int nodeCount) {
n = nodeCount;
adjList = new list<node>[n];
}
void addEdge(int source, int dest, int cost) {
node newNode;
newNode.dest = dest;
newNode.cost = cost;
adjList[source].push_back(newNode);
}
void displayEdges() {
for(int i = 0; i<n; i++) {
list<node> tempList = adjList[i];
showList(i, tempList);
}
}
friend void dijkstra(Graph g, int *dist, int *prev, int start);
};
void dijkstra(Graph g, int *dist, int *prev, int start) {
int n = g.n;
for(int u = 0; u<n; u++) {
dist[u] = 9999; //set as infinity
prev[u] = -1; //undefined previous
}
dist[start] = 0; //distance of start is 0
set<int> S; //create empty set S
list<int> Q;
for(int u = 0; u<n; u++) {
Q.push_back(u); //add each node into queue
}
while(!Q.empty()) {
list<int> :: iterator i;
i = min_element(Q.begin(), Q.end());
int u = *i; //the minimum element from queue
Q.remove(u);
S.insert(u); //add u in the set
list<node> :: iterator it;
for(it = g.adjList[u].begin(); it != g.adjList[u].end();it++) {
if((dist[u]+(it->cost)) < dist[it->dest]) { //relax (u,v)
dist[it->dest] = (dist[u]+(it->cost));
prev[it->dest] = u;
}
}
}
}
main() {
int n = 7;
Graph g(n);
int dist[n], prev[n];
int start = 0;
g.addEdge(0, 1, 3);
g.addEdge(0, 2, 6);
g.addEdge(1, 0, 3);
g.addEdge(1, 2, 2);
g.addEdge(1, 3, 1);
g.addEdge(2, 1, 6);
g.addEdge(2, 1, 2);
g.addEdge(2, 3, 1);
g.addEdge(2, 4, 4);
g.addEdge(2, 5, 2);
g.addEdge(3, 1, 1);
g.addEdge(3, 2, 1);
g.addEdge(3, 4, 2);
g.addEdge(3, 6, 4);
g.addEdge(4, 2, 4);
g.addEdge(4, 3, 2);
g.addEdge(4, 5, 2);
g.addEdge(4, 6, 1);
g.addEdge(5, 2, 2);
g.addEdge(5, 4, 2);
g.addEdge(5, 6, 1);
g.addEdge(6, 3, 4);
g.addEdge(6, 4, 1);
g.addEdge(6, 5, 1);
dijkstra(g, dist, prev, start);
for(int i = 0; i<n; i++)
if(i != start)
cout<<start<<" to "<<i<<", Cost: "<<dist[i]<<" Previous: "<<prev[i]<<endl;
} Đầu ra
0 to 1, Cost: 3 Previous: 0 0 to 2, Cost: 5 Previous: 1 0 to 3, Cost: 4 Previous: 1 0 to 4, Cost: 6 Previous: 3 0 to 5, Cost: 7 Previous: 2 0 to 6, Cost: 7 Previous: 4
