Thảo luận về việc chia một số nguyên không dấu bằng cách sử dụng một thuật toán chia. Một số thuật toán phân chia được áp dụng trên giấy, và một số thuật toán khác được thực hiện trên các mạch kỹ thuật số. Thuật toán chia có hai loại:thuật toán chia chậm và giải thuật chia nhanh. Thuật toán phân chia chậm bao gồm thuật toán khôi phục, khôi phục không thực hiện, SRT và không khôi phục.
Trong hướng dẫn này, chúng ta sẽ thảo luận về thuật toán Khôi phục, giả sử rằng 0
Trong phần này, chúng ta sẽ sử dụng thanh ghi Q để lưu trữ thương, thanh ghi A để lưu trữ phần dư và M để lưu trữ số chia. Giá trị ban đầu của A được giữ bằng 0 và giá trị của nó được khôi phục, đó là lý do tại sao phương pháp này khôi phục phép chia.
Khởi tạo các thanh ghi với các giá trị,
Q =Cổ tức,
A =0,
M =số chia,
N =số bit cổ tức.
Dịch chuyển trái AQ có nghĩa là lấy thanh ghi A và Q làm một đơn vị duy nhất.
Trừ A với M và lưu trữ trong A.
Kiểm tra bit quan trọng nhất của A:
Nếu nó là 0, hãy đặt bit quan trọng nhất thành 1.
Nếu không, hãy đặt bit quan trọng nhất thành 0.
Khôi phục giá trị của A và giảm giá trị của bộ đếm N.
Nếu N =0, ngắt vòng lặp; nếu không, hãy chuyển sang bước 2.
Thương số được lưu trữ trong thanh ghi Q.
Mã C ++ cho phương pháp tiếp cận trên
Trong hướng dẫn này, chúng tôi đã thảo luận về Thuật toán chia khôi phục cho một số nguyên không dấu. Chúng tôi đã thảo luận về một cách tiếp cận đơn giản để giải quyết vấn đề này với sự trợ giúp của biểu đồ luồng và áp dụng các phép toán bit. Chúng tôi cũng đã thảo luận về chương trình C ++ cho vấn đề này mà chúng tôi có thể làm với các ngôn ngữ lập trình như C, Java, Python, v.v. Chúng tôi hy vọng bạn thấy hướng dẫn này hữu ích. Phương pháp tiếp cận để tìm giải pháp
Lưu đồ
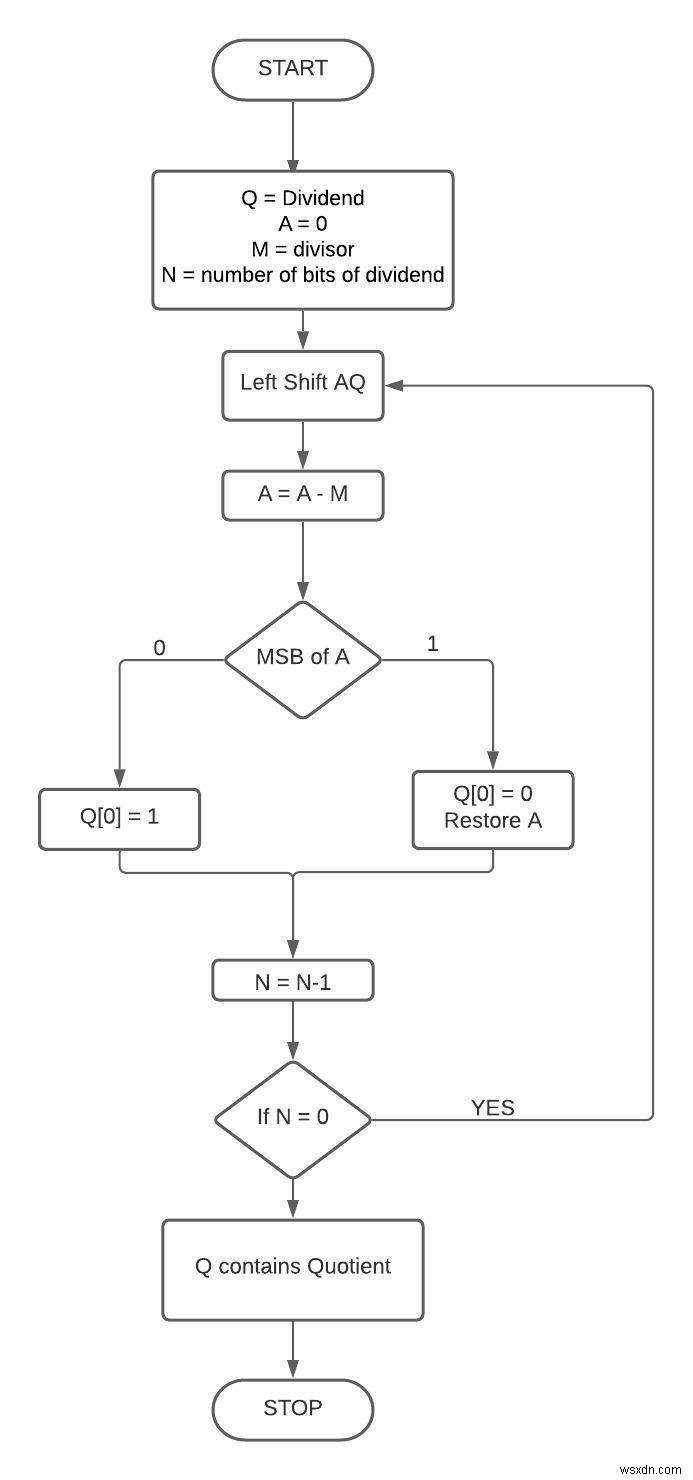
Ví dụ
#include <iostream>
using namespace std;
int main(){
// initializing all the variables with Dividend = 9, Divisor = 2.
int Q = 8,q=1,M=3;
short N = 4;
int A = Q;
M <<= N;
// loop for division by bit operation.
for(int i=N-1; i>=0; i--) {
A = (A << 1)- M;
// checking MSB of A.
if(A < 0) {
q &= ~(1 << i); // set i-th bit to 0
A = A + M;
} else {
q |= 1 << i; // set i-th bit to 1
}
}
cout << "Quotient: "<< q;
return 0;
} Đầu ra
Quotient: 2
Kết luận
