Thuật toán Fleury được sử dụng để hiển thị đường dẫn Euler hoặc mạch Euler từ một đồ thị nhất định. Trong thuật toán này, bắt đầu từ một cạnh, nó cố gắng di chuyển các đỉnh liền kề khác bằng cách loại bỏ các đỉnh trước đó. Sử dụng thủ thuật này, biểu đồ sẽ trở nên đơn giản hơn trong mỗi bước để tìm đường dẫn hoặc mạch Euler.
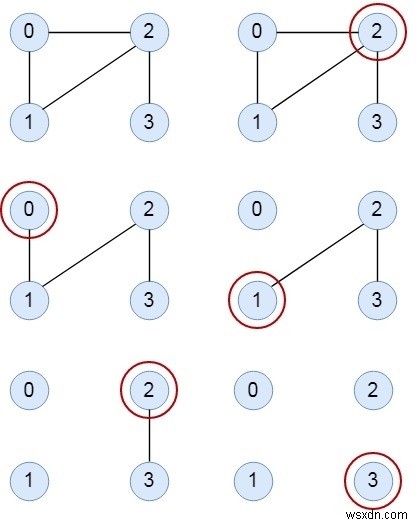
Chúng tôi phải kiểm tra một số quy tắc để lấy đường dẫn hoặc mạch -
- Biểu đồ phải là Đồ thị Euler.
- Khi có hai cạnh, một cạnh là cầu, một cạnh khác không phải là cầu, lúc đầu chúng ta phải chọn không cầu. s
Việc chọn đỉnh xuất phát cũng khó, ta không thể dùng đỉnh nào làm đỉnh xuất phát, nếu đồ thị không có đỉnh bậc lẻ thì ta có thể chọn đỉnh bất kỳ làm điểm bắt đầu, ngược lại khi một đỉnh có bậc lẻ thì ta phải chọn đỉnh đó trước. .
Đầu vào - Ma trận kề của đồ thị
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Đầu ra - Đường dẫn hoặc mạch Euler:1--0 0--2 2--1 1--3 3--0 0--4 4--3 3—2
Thuật toán
findStartVert(graph) Input: The given graph. Output: Find the starting vertex to start algorithm. Begin for all vertex i, in the graph, do deg := 0 for all vertex j, which are adjacent with i, do deg := deg + 1 done if deg is odd, then return i done when all degree is even return 0 End isBridge(u, v) Input: The start and end node. Output: True when u and v are forming a bridge. Begin deg := 0 for all vertex i which are adjacent with v, do deg := deg + 1 done if deg > 1, then return false return true End fleuryAlgorithm(start) Input: The starting vertex. Output: Display the Euler path or circuit. Begin edge := get the number of edges in the graph //it will not initialize in next recursion call for all vertex v, which are adjacent with start, do if edge <= 1 OR isBridge(start, v) is false, then display path from start and v remove edge (start,v) from the graph decrease edge by 1 fleuryAlgorithm(v) done End
Ví dụ
#include<iostream>
#include<vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 1, 1},
{1, 0, 1, 1, 0},
{1, 1, 0, 1, 0},
{1, 1, 1, 0, 1},
{1, 0, 0, 1, 0}
};
int tempGraph[NODE][NODE];
int findStartVert(){
for(int i = 0; i<NODE; i++){
int deg = 0;
for(int j = 0; j<NODE; j++){
if(tempGraph[i][j])
deg++; //increase degree, when connected edge found
}
if(deg % 2 != 0) //when degree of vertices are odd
return i; //i is node with odd degree
}
return 0; //when all vertices have even degree, start from 0
}
bool isBridge(int u, int v){
int deg = 0;
for(int i = 0; i<NODE; i++)
if(tempGraph[v][i])
deg++;
if(deg>1){
return false; //the edge is not forming bridge
}
return true; //edge forming a bridge
}
int edgeCount(){
int count = 0;
for(int i = 0; i<NODE; i++)
for(int j = i; j<NODE; j++)
if(tempGraph[i][j])
count++;
return count; //count nunber of edges in the graph
}
void fleuryAlgorithm(int start){
static int edge = edgeCount();
for(int v = 0; v<NODE; v++){
if(tempGraph[start][v]){ //when (u,v) edge is presnt and not forming bridge
if(edge <= 1 || !isBridge(start, v)){
cout << start << "--" << v << " ";
tempGraph[start][v] = tempGraph[v][start] = 0; //remove edge from graph
edge--; //reduce edge
fleuryAlgorithm(v);
}
}
}
}
int main(){
for(int i = 0; i<NODE; i++) //copy main graph to tempGraph
for(int j = 0; j<NODE; j++)
tempGraph[i][j] = graph[i][j];
cout << "Euler Path Or Circuit: ";
fleuryAlgorithm(findStartVert());
} Đầu ra
Euler Path Or Circuit: 1--0 0--2 2--1 1--3 3--0 0--4 4--3 3—2
