Giả sử chúng ta có một hình chữ nhật ABCD, nhưng chúng ta chỉ có tọa độ của trung điểm P và Q, và chiều dài của hình chữ nhật L.
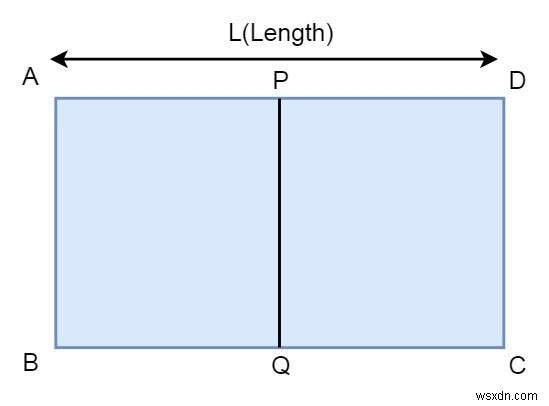
Nhiệm vụ của chúng ta là tìm tọa độ của A, B, C và D bằng cách sử dụng tọa độ của P và Q, và độ dài của cạnh L. Ví dụ, nếu P là (1, 0) và Q là (1, 2) , và L là 2, thì A, B, C, D sẽ lần lượt là (0, 0), (0, 2), (2, 2). (2, 0).
Có thể có ba trường hợp có thể xảy ra.
- Hình chữ nhật nằm ngang nên AD và BC song song với trục X
- Hình chữ nhật là hình chữ nhật thẳng đứng, do đó AD và BC song song với trục Y
- Hình chữ nhật nghiêng một góc nhất định với các trục.
Đối với trường hợp thứ ba, ta phải tìm hệ số góc bằng cách sử dụng tọa độ của P và Q. Nếu ta được hệ số góc của AD thì ta có thể lập phương trình đường thẳng đi qua AD, sau đó sử dụng công thức khoảng cách ta sẽ được kết quả.
$$ Độ dốc của AD, m =\ frac {px-qx} {py-qy} $$ $$ Displacement \:vertical \:x \:axis, dx =\ frac {L} {2 \ sqrt {1 + m ^ {2}}} $$ $$ Displacement \:vertical \:y \:axis, dy =\ frac {mL} {2 \ sqrt {1 + m ^ {2}}} $$
Ví dụ
#include <iostream>
#include <cmath>
using namespace std;
class Point {
public:
float x, y;
Point(float a = 0.0f, float b = 0.0f) {
x = a, y = b;
}
};
void printCorners(Point p, Point q, float l) {
Point a, b, c, d;
if (p.x == q.x) {
a.x = p.x - (l/2.0);
d.x = p.x + (l/2.0);
a.y = d.y = p.y;
b.x = q.x - (l/2.0);
c.x = q.x + (l/2.0);
b.y = c.y = q.y;
}else if (p.y == q.y) {
a.y = p.y - (l/2.0);
d.y = p.y + (l/2.0);
a.x = d.x = p.x;
b.y = q.y - (l/2.0);
c.y = q.y + (l/2.0);
b.x = c.x = q.x;
}else{
float m = (p.x-q.x)/float(q.y-p.y);
float dx = (l /sqrt(1+(m*m))) *0.5 ;
float dy = m*dx;
a.x = p.x - dx;
a.y = p.y - dy;
d.x = p.x + dx;
d.y = p.y + dy;
b.x = q.x - dx;
b.y = q.y - dy;
c.x = q.x + dx;
c.y = q.y + dy;
}
cout << "A (" << a.x << ", " << a.y << ")\n"
<< "B (" << b.x << ", " << b.y << ")\n"
<< "C (" << c.x << ", " << c.y << ")\n"
<< "D (" << d.x << ", " << d.y << ")\n";
}
int main() {
Point p(1, 1), q(-1, -1);
printCorners(p, q, 2*sqrt(2));
} Đầu ra
A (0, 2) B (-2, 0) C (0, -2) D (2, 0)
