Tìm số lượng tứ giác có thể có từ các điểm cho trước bằng cách sử dụng C ++

Một tứ giác tạo thành một đa giác có bốn đỉnh và bốn cạnh trong hình học phẳng Euclide. Tên 4-gon, v.v. Được bao gồm trong các tên khác của tứ giác và đôi khi chúng còn được gọi là hình vuông, kiểu hiển thị, v.v.

Trong bài viết này, chúng tôi sẽ giải thích các cách tiếp cận để tìm số lượng các tứ giác có thể có từ các điểm đã cho. Trong bài toán này, chúng ta cần tìm xem có bao nhiêu tứ giác có thể tạo ra với bốn điểm (x, y) đã cho trong mặt phẳng macte. Vì vậy, đây là ví dụ cho vấn đề đã cho -

 Đầu vào:A (-2, 8), B (-2, 0), C (6, -1), D (0, 8) Đầu ra:1> 
  
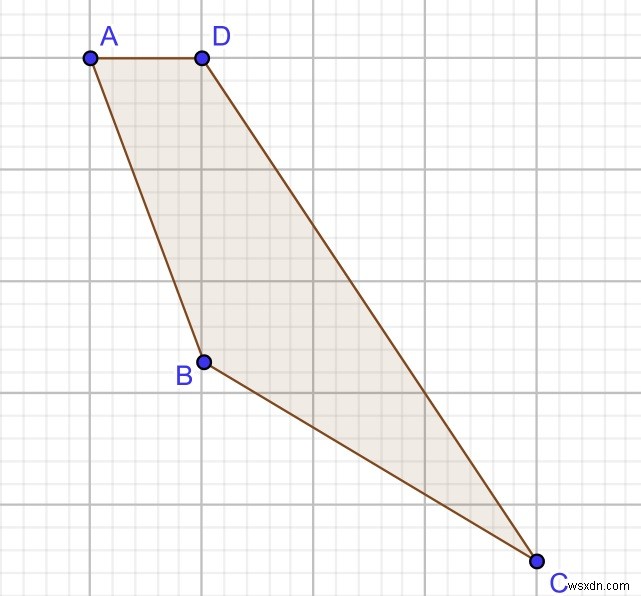  Đầu vào:A (1, 8), B (0, 1), C (4, 0), D (1, 2) Đầu ra:3 Hình phẳng:3 tứ giác có thể được tạo thành (ABCD), (ABDC) và ( ADBC). 
  Phương pháp tiếp cận để tìm giải pháp 
   
 Trước tiên, chúng tôi sẽ kiểm tra xem 3 trong số 4 điểm có thẳng hàng hay không và nếu có thì  không có tứ giác nào có thể được tạo thành với các điểm  . 
 
  
 Sau đó, chúng tôi sẽ kiểm tra xem 2 trong số 4 điểm có giống nhau không và nếu có thì  không có tứ giác nào có thể được tạo thành  . 
 
  
 Bây giờ, chúng ta sẽ kiểm tra xem đường chéo có cắt nhau hay không. Nếu có, thì chỉ có  một tứ giác có thể được tạo thành,  được gọi là  tứ giác lồi  . 
 
 
 
  
 
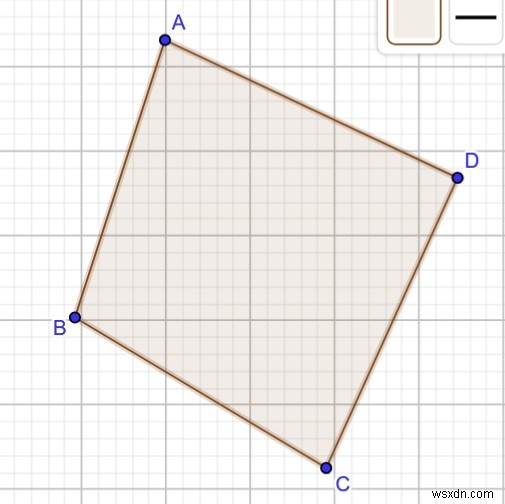
 Tổng số giao lộ =1 
 
 Nếu các đường chéo không cắt nhau thì có thể tạo thành ba tứ giác có thể có, gọi là tứ giác lõm. 
 
  
 
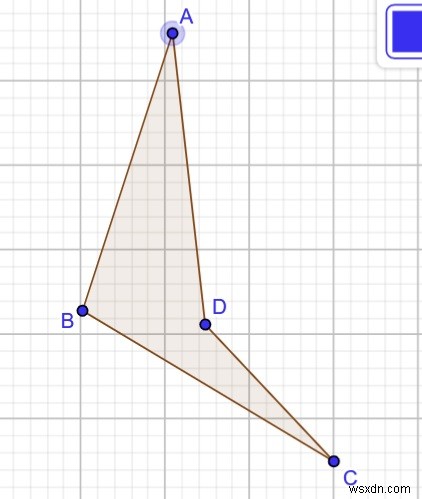
 Tổng số giao lộ =0 
  Ví dụ 
  #include  using namespace std; struct Point {// points int x; int y;}; int check_orientation (Point i, Point j, Point k) {int val =(j.y - i.y) * (k.x - j.x) - (j.x - i.x) * (k.y - j.y); if (val ==0) return 0; trả về (val> 0)? 1:2;} // kiểm tra xem các đoạn thẳng có giao nhau hay không check_Intersect (Điểm A, Điểm B, Điểm C, Điểm D) {int o1 =check_orientation (A, B, C); int o2 =check_orientation (A, B, D); int o3 =check_orientation (C, D, A); int o4 =check_orientation (C, D, B); if (o1! =o2 &&o3! =o4) trả về true; return false;} // kiểm tra xem 2 điểm có giống nhau hay không. có thể được hình thành nếu (A.x ==B.x &&A.y ==B.y) return false; // trả về true cho không tìm thấy tương tự return true;} // Kiểm tra tính cộng tuyến của ba pointbool check_collinear (Point A, Point B, Point C) {int x1 =A.x, y1 =A.y; int x2 =B.x, y2 =B.y; int x3 =C.x, y3 =C.y; if ((y3 - y2) * (x2 - x1) ==(y2 - y1) * (x3 - x2)) return false; else return true;} // hàm main hàm main () {struct Point A, B, C, D; A.x =-2, A.y =8; // A (-2, 8) B.x =-2, B.y =0; // B (-2, 0) C.x =6, C.y =-1; // C (6 , -1) D.x =0, D.y =8; // D (0, 8) // Kiểm tra xem 3 điểm có thẳng hàng bool hay không flag =true; flag =flag &check_collinear (A, B, C); flag =flag &check_collinear (A, B, D); flag =flag &check_collinear (A, C, D); flag =flag &check_collinear (B, C, D); // Nếu các điểm tìm thấy thẳng hàng if (flag ==false) {cout <<"Số tứ giác có thể có từ các điểm đã cho:0"; trả về 0; } // Kiểm tra xem 2 điểm có giống nhau không. bool same =true; same =same &check_similar (A, B); same =same &check_similar (A, C); same =same &check_similar (B, D); same =same &check_similar (C, D); same =same &check_similar (A, D); same =same &check_similar (B, C); // Nếu tồn tại điểm tương tự if (same ==false) {cout <<"Số tứ giác có thể có từ các điểm đã cho:0"; trả về 0; } // kiểm tra xem đường chéo có cắt nhau hay không flag =true; if (check_Intersect (A, B, C, D)) flag =false; if (check_Intersect (A, C, B, D)) flag =false; if (check_Intersect (A, B, D, C)) flag =false; if (flag ==true) cout <<"Số tứ giác có thể có từ các điểm đã cho:3"; else cout <<"Số tứ giác có thể có từ các điểm đã cho:1"; trả về 0;} 
  Đầu ra 
  Số tứ giác có thể có từ các điểm đã cho:1 
  Giải thích về Quy tắc trên 
 
 Bạn có thể hiểu mã này theo các bước sau - 
   
 Kiểm tra xem ba điểm bất kỳ có thẳng hàng hay không và nếu có, thì đó là số của một phần tư. :0 
 
  
 Kiểm tra xem hai điểm bất kỳ có giống nhau không và nếu có, thì đó là số của một phần tư. :0 
 
  
 Kiểm tra xem có đoạn đường nào cắt nhau không:
   
 Nếu có, thì số của một phần tư. :1 
 
  
 Nếu không, thì số lượng quads. :3 
 
 
 
 
  Kết luận 
 
 Trong bài này, chúng tôi đã giải quyết việc tìm tất cả các tứ giác có thể tạo thành từ 4 điểm đã cho. Chúng tôi hiểu số lượng các tứ giác phụ thuộc như thế nào vào tính thẳng hàng, giao điểm và hướng. Chúng tôi cũng viết các chương trình C ++ tương tự và chúng tôi có thể viết chương trình này bằng bất kỳ ngôn ngữ nào khác như C, Java và python.