Hãy xem xét chúng ta có một tập hợp các điểm. Chúng ta phải tìm một con đường khép kín đơn giản bao gồm tất cả các điểm. Giả sử các điểm giống như bên dưới và hình ảnh tiếp theo đang tạo một đường khép kín trên các điểm đó.
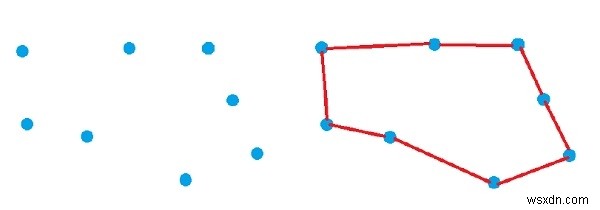
Để có được đường dẫn, chúng ta phải làm theo các bước sau -
-
Tìm điểm dưới cùng bên trái là P
-
Sắp xếp n - 1 điểm khác dựa trên góc phân cực ngược chiều kim đồng hồ quanh P, nếu góc cực của hai điểm bằng nhau thì xếp chúng sao cho khoảng cách là ngắn nhất
-
Duyệt qua danh sách các điểm đã được sắp xếp, sau đó tạo đường dẫn
Ví dụ
#include <bits/stdc++.h>
using namespace std;
class Point {
public:
int x, y;
};
Point p0;
int euclid_dist(Point p1, Point p2) {
return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}
int orientation(Point p1, Point p2, Point p3) {
int val = (p2.y - p1.y) * (p3.x - p2.x) - (p2.x - p1.x) * (p3.y - p2.y);
if (val == 0) return 0; // colinear
return (val > 0)? 1: 2; // clockwise or counterclock wise
}
int compare(const void *vp1, const void *vp2) {
Point *p1 = (Point *)vp1;
Point *p2 = (Point *)vp2;
int o = orientation(p0, *p1, *p2);
if (o == 0)
return (euclid_dist(p0, *p2) >= euclid_dist(p0, *p1))? -1 : 1;
return (o == 2)? -1: 1;
}
void findClosedPath(Point points[], int n) {
int y_min = points[0].y, min = 0;
for (int i = 1; i < n; i++) {
int y = points[i].y;
if ((y < y_min) || (y_min == y && points[i].x < points[min].x))
y_min = points[i].y, min = i;
}
swap(points[0], points[min]);
p0 = points[0];
qsort(&points[1], n-1, sizeof(Point), compare); //sort on polar angle
for (int i=0; i<n; i++)
cout << "(" << points[i].x << ", "<< points[i].y <<"), ";
}
int main() {
Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},{0, 0}, {1, 2}, {3, 1}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
findClosedPath(points, n);
} Đầu ra
(0, 0), (3, 1), (1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (0, 3),
