Cây 2-3 được định nghĩa là cấu trúc dữ liệu dạng cây, trong đó mỗi nút có con (nút bên trong) có hai con (2 nút) cũng như một phần tử dữ liệu hoặc ba con (3 nút) cũng như hai dữ liệu. các phần tử.
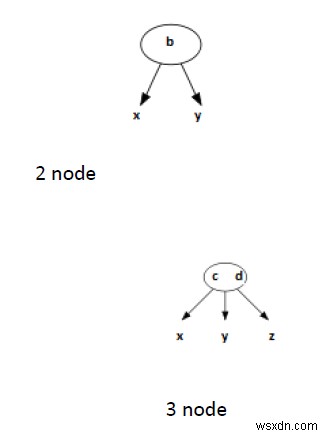
Định nghĩa
Chúng tôi gọi rằng một nút bên trong là một nút 2 nếu nó có một phần tử dữ liệu và hai phần tử con.
Chúng tôi gọi rằng một nút bên trong là nút 3 nếu nó có hai phần tử dữ liệu và ba phần tử con.
Chúng tôi gọi rằng T là cây 2-3 nếu và chỉ khi một trong các câu sau thỏa mãn -
-
T còn trống hoặc trống. Nói cách khác, T chứa không có bất kỳ nút nào.
-
T là 2 nút được trang bị phần tử dữ liệu a. Nếu T có con trái L và con phải R thì ta kết luận
-
L và R được coi là 2-3 cây không trống có cùng chiều cao;
-
a cao hơn mỗi phần tử trong L; và
-
a nhỏ hơn hoặc bằng mỗi phần tử dữ liệu trong R.
-
T là một nút 3 với các phần tử dữ liệu a và b, trong đó a nhỏ hơn b. Nếu T có con trái L, con giữa M và con phải R thì ta kết luận
-
L, M và R được coi là 2-3 cây không trống có chiều cao bằng nhau;
-
a cao hơn mỗi phần tử dữ liệu trong L và nhỏ hơn hoặc bằng mỗi phần tử dữ liệu trong M; và
-
b cao hơn mỗi phần tử dữ liệu trong M và nhỏ hơn hoặc bằng mỗi phần tử dữ liệu trong R.
Thuộc tính
-
Mọi nút bên trong được coi là 2 nút hoặc 3 nút.
-
Tất cả các lá nằm ở cùng một mức.
-
Tất cả dữ liệu được duy trì hoặc lưu giữ theo thứ tự được sắp xếp.
Hoạt động
Tìm kiếm
Tìm kiếm một mục trong cây 2-3 cũng giống như tìm kiếm một mục trong cây tìm kiếm nhị phân. Vì các phần tử dữ liệu trong mỗi nút được coi là có thứ tự, một hàm tìm kiếm sẽ được chuyển hướng đến đúng cây con và cuối cùng đến đúng nút chứa mục.
-
Gọi T là cây 2-3 và d là phần tử dữ liệu chúng ta muốn tìm. Nếu T trống, thì d không có trong T và chúng ta được thực hiện.
-
Hãy coi r là gốc của T.
-
Gọi r là một chiếc lá. Nếu d không nằm trong r, kết quả là d không thuộc T. Ngược lại, d nằm trong T. Đặc biệt, có thể tìm thấy d ở một nút lá. Chúng tôi không cần thêm bước nào nữa và chúng tôi đã được thực hiện.
-
Giả sử r được coi là nút 2 nút với nút con bên trái L và nút con bên phải R. Gọi e được coi là phần tử dữ liệu trong r.
Có ba trường hợp -
-
Nếu d bằng e, thì chúng ta đã tìm thấy d trong T và chúng ta được biểu diễn.
-
Nếu d nhỏ hơn e, thì đặt T thành L, theo định nghĩa là cây 2-3 và quay lại bước 2.
-
Nếu d lớn hơn e, thì đặt T thành R và quay lại bước 2.
-
Gọi r là 3 nút với nút con trái L, nút con giữa M và nút con phải R. Gọi a và b là hai phần tử dữ liệu của r, trong đó a
-
Nếu d bằng a hoặc b thì d nằm trong T và chúng ta được thực hiện.
-
Nếu d nhỏ hơn a, thì đặt T thành L và quay lại bước 2.
-
Nếu ais nhỏ hơn d và d nhỏ hơn b, thì đặt T thành M và quay lại bước 2.
-
Nếu d lớn hơn b, sau đó đặt T thành R và quay trở lại bước 2.
-
Chèn
Chèn thực hiện bằng cách tìm kiếm vị trí thích hợp của khóa và thêm hoặc thêm vào đó. Nếu nút trở thành 4 nút thì nút đó được chia thành hai nút 2 và khóa ở giữa được chuyển lên cha mẹ. Sau đó, nút cha có thể trở thành một nút 4, trong trường hợp đó, nó cũng được chia, truyền một khóa đến nút cha của chính nó. Quá trình này lặp lại cho đến khi và trừ khi chúng ta đến phần tử gốc là 2 nút và không cần chia hoặc khi chúng tôi đến gốc, trong trường hợp đó, chúng tôi triển khai phần tử được truyền để tạo một gốc mới là 2 nút . Với sự trợ giúp của thuật toán này, số lượng phép toán cần thực hiện tỷ lệ với chiều cao của cây, do đó tính logarit vì cây được cân bằng hoàn hảo. Quá trình này đảm bảo rằng kết quả của nó được coi là một cây 2-3:đặc biệt, tất cả các lá vẫn ở cùng độ sâu.
Sơ đồ dưới đây giải thích hoặc minh họa các trường hợp có thể xảy ra của quá trình này.
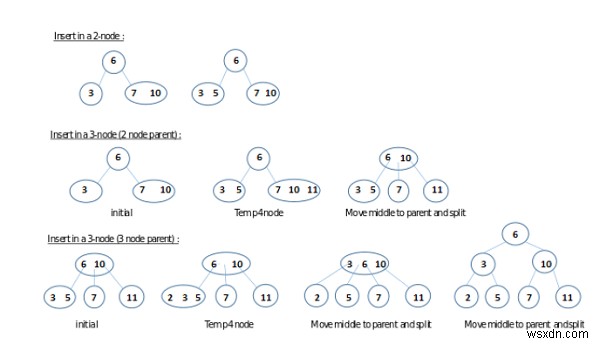
Chèn một số vào cây 2-3 cho 3 trường hợp có thể xảy ra.
