Cho f =(x1 ∨ y1) ∧ (x2 ∨ y2) ∧ ... ∧ (xn ∨ yn).
Vấn đề:Liệu f có thỏa mãn không?
xi ∨ yi và  và
và 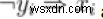
đều tương đương. Vì vậy, chúng tôi đang chuyển đổi mỗi (xi ∨ yi) thành hai câu lệnh đó.
Bây giờ giả sử một đồ thị có 2n đỉnh. Trong trường hợp mỗi (xi∨yi) hai cạnh có hướng được thêm vào
-
Từ ¬xi đến yi
-
Từ ¬yi sang xi
f không được coi là thỏa mãn nếu cả ¬xi và xi đều ở trong cùng một SCC (Thành phần được kết nối mạnh mẽ)
Giả sử rằng f được coi là thỏa mãn. Bây giờ chúng ta muốn cung cấp các giá trị cho mỗi biến để thỏa mãn f. Nó có thể được thực hiện với một loại đỉnh tôpô của đồ thị mà chúng ta xây dựng. Nếu ¬xi đứng sau xi trong loại tôpô, xi phải được coi là FALSE. Nếu không, nó phải được coi là ĐÚNG.
Mã giả
func dfsFirst1(vertex v1): marked1[v1] = true for each vertex u1 adjacent to v1 do: if not marked1[u1]: dfsFirst1(u1) stack.push(v1) func dfsSecond1(vertex v1): marked1[v1] = true for each vertex u1 adjacent to v1 do: if not marked1[u1]: dfsSecond1(u1) component1[v1] = counter for i = 1 to n1 do: addEdge1(not x[i], y[i]) addEdge1(not y[i], x[i]) for i = 1 to n1 do: if not marked1[x[i]]: dfsFirst1(x[i]) if not marked1[y[i]]: dfsFirst1(y[i]) if not marked1[not x[i]]: dfsFirst1(not x[i]) if not marked1[not y[i]]: dfsFirst1(not y[i]) set all marked values false counter = 0 flip directions of edges // change v1 -> u1 to u1 -> v1 while stack is not empty do: v1 = stack.pop if not marked1[v1] counter = counter + 1 dfsSecond1(v1) for i = 1 to n1 do: if component1[x[i]] == component1[not x[i]]: it is unsatisfiable exit if component1[y[i]] == component1[not y[i]]: it is unsatisfiable exit it is satisfiable exit
