Đặt trước Traversal của N-ary Tree không có đệ quy trong C ++

Trong bài toán này, chúng ta được đưa ra một N-ary Tree. Nhiệm vụ của chúng tôi là in đường đi ngang của cây được đặt hàng trước.

Trước tiên, chúng ta hãy tìm hiểu một số thuật ngữ cơ bản,

Cây N-ary là một cây trong đó tất cả các nút có thể có tối đa N nút con. Ví dụ cây 2-ary (nhị phân) có tối đa 2 nút con.

Đặt hàng trước Truyền tải là một cách để đi qua các nút của cây. Trong phần này, đầu tiên chúng ta sẽ duyệt qua nút gốc, sau đó là nút con bên trái và sau đó là nút con bên phải.

Hãy lấy một ví dụ để hiểu vấn đề của chúng ta

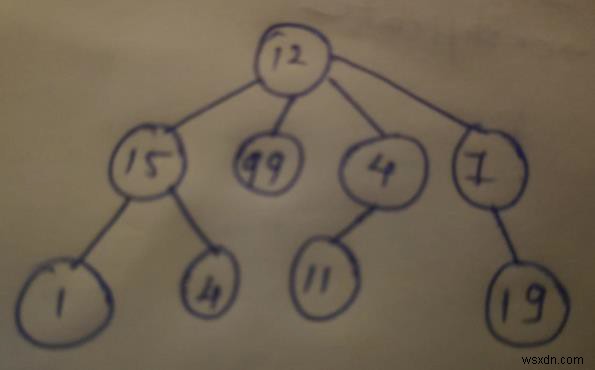
Preorder traversal :
12151499411719

Để giải quyết vấn đề này, chúng ta phải sử dụng cấu trúc dữ liệu ngăn xếp. Đầu tiên chúng ta sẽ đẩy nút gốc vào ngăn xếp. Sau đó mở nó ra và in nó. Đối với mọi nút bật lên, chúng ta sẽ đẩy các nút con của ngăn xếp từ nút con bên phải sang nút con bên trái. Sau đó bật lên khi tất cả các nút con được đẩy. Lặp lại quá trình này cho đến khi ngăn xếp trống.

Chương trình cho thấy việc triển khai giải pháp của chúng tôi

Ví dụ

#include <bits/stdc++.h>
using namespace std;
struct Node {
   int key;
   vector<Node*> child;
};
Node* insertNode(int key){
   Node* temp = new Node;
   temp->key = key;
   return temp;
}
void preOrderTraversal(struct Node* root){
   stack<Node*> tree;
   tree.push(root);
   while (!tree.empty()) {
      Node* curr = tree.top();
      tree.pop();
      cout<<curr->key<<"\t";
      vector<Node*>::iterator it = curr->child.end();
      while (it != curr->child.begin()) {
         it--;
         tree.push(*it);
      }
   }
}
int main(){
   Node* root = insertNode(12);
   (root->child).push_back(insertNode(15));
   (root->child).push_back(insertNode(99));
   (root->child).push_back(insertNode(4));
   (root->child).push_back(insertNode(7));
   (root->child[0]->child).push_back(insertNode(1));
   (root->child[0]->child).push_back(insertNode(4));
   (root->child[0]->child).push_back(insertNode(25));
   (root->child[2]->child).push_back(insertNode(11));
   (root->child[3]->child).push_back(insertNode(19));
   cout<<"PreOrder Traversal of the tree is :\n";
   preOrderTraversal(root);
   return 0;
}

Đầu ra

PreOrder Traversal of the tree is :
12   15   14   25   99   4   11   7   19