Cây con kích thước chẵn trong cây n-ary trong C ++

Trong bài toán này, chúng ta được đưa ra một danh sách kề biểu thị một cây n-ary. Nhiệm vụ của chúng ta là tìm số cây con có kích thước chẵn trong cây n-ary.

N-ary tree được định nghĩa là một tập hợp các nút thường được trình bày phân cấp theo cách sau.

Cây được bắt đầu ở nút gốc.

Mỗi nút của cây duy trì một danh sách các con trỏ đến các nút con của nó.

Số lượng nút con nhỏ hơn hoặc bằng m.

Hãy lấy một ví dụ để hiểu vấn đề,

Đầu vào:

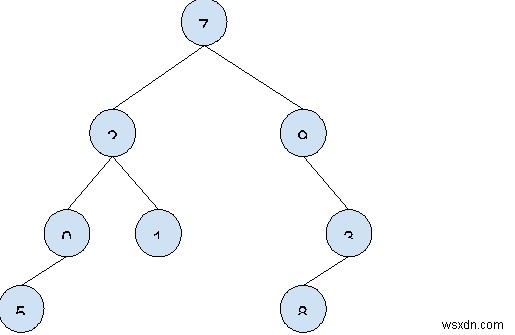
Đầu ra: 4

Giải thích:

Cây có gốc bằng 7 có kích thước đều nhau.
Cây có 2 gốc có kích thước đều nhau.
Cây có gốc bằng 0 có kích thước chẵn.
Cây có 3 gốc có kích thước đều nhau.

Phương pháp tiếp cận giải pháp -

Một cách tiếp cận đơn giản là đếm tất cả các nút con cho một nút nhất định, nếu nó thậm chí làm tăng Số tiền chẵn. Đối với điều này, chúng tôi sẽ sử dụng DFS và tìm độ dài của SubTree cho nút đã cho.

Chúng ta có thể làm điều này bằng cách sử dụng một đường đi ngang trên cây. Bằng cách tìm kiếm một cách đệ quy kích thước của các cây con của mỗi nút con, sau đó kiểm tra kích thước và nếu nó là số chẵn, hãy tăng Số lượng chẵn nếu không thì hãy để nguyên.

Chương trình minh họa hoạt động của giải pháp của chúng tôi,

Ví dụ

#include <bits/stdc++.h>
using namespace std;

int countEventSizeSubTree(vector<int> adj[], int n, int v, int&amp; EvenCount){

   int size = 1;
   for (auto ele : adj[v]) {
      size += countEventSizeSubTree(adj, n, ele, EvenCount);
   }
   if (size % 2 == 0)
      EvenCount++;
   return size;
}

int main(){

   int n;
   n = 10;

   vector<int> adj[n + 1];
   adj[7].push_back(2);
   adj[7].push_back(9);
   adj[2].push_back(0);
   adj[2].push_back(1);
   adj[9].push_back(3);
   adj[3].push_back(8);
   adj[0].push_back(5);

   int EvenCount = 0;
   countEventSizeSubTree(adj, n, 1, EvenCount);
   cout<<"Even Size SubTree are "<<EvenCount;
   return 0;
}

Đầu ra -

Even Size SubTree are 0