Trong bài toán này, chúng tôi được cung cấp một cây nhị phân và chúng tôi được yêu cầu thực hiện dfs từ một nút cụ thể, trong đó chúng tôi giả sử nút đã cho là gốc và thực hiện dfs từ nó.
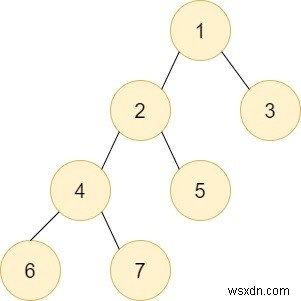
Trong cây trên, giả sử chúng ta được yêu cầu thực hiện DFS từ nút F
Trong hướng dẫn này, chúng tôi sẽ áp dụng một số phương pháp không chính thống để nó sẽ giảm đáng kể độ phức tạp về thời gian của chúng tôi và do đó chúng tôi sẽ có thể chạy mã này cho các ràng buộc cao hơn.
Phương pháp tiếp cận - Trong cách tiếp cận này, chúng tôi sẽ không đơn giản đi theo cách ngây thơ, tức là chúng tôi chỉ áp dụng dfs cho mọi nút vì nó sẽ không hoạt động đối với các ràng buộc cao hơn, vì vậy chúng tôi cố gắng sử dụng một số phương pháp không chính thống để tránh nhận được TLE.
#include <bits/stdc++.h>
using namespace std;
#define N 100000
// Adjacency list to store the
// tree nodes connections
vector<int> v[N];
unordered_map<int, int> mape; // will be used for associating the node with it's index
vector<int> a;
void dfs(int nodesunder[], int child, int parent){ // function for dfs and precalculation our nodesunder
a.push_back(child); // storing the dfs of our tree
// nodesunder of child subtree
nodesunder[child] = 1;
for (auto it : v[child]) { // performing normal dfs
if (it != parent) { // as we the child can climb up to
//it's parent so we are trying to avoid that as it will become a cycle
dfs(nodesunder, it, child); // recursive call
nodesunder[child] += nodesunder[it]; // storing incrementing the nodesunder
//by the number of nodes under it's children
}
}
}
// Function to print the DFS of subtree of node
void printDFS(int node, int nodesunder[]){
int ind = mape[node]; // index of our node in the dfs array
cout << "The DFS of subtree " << node << ": ";
// print the DFS of subtree
for (int i = ind; i < ind + nodesunder[node]; i++){ // going through dfs array and then
//printing all the nodes under our given node
cout << a[i] << " ";
}
cout << endl;
}
void addEdgetoGraph(int x, int y){ // for maintaining adjacency list
v[x].push_back(y);
v[y].push_back(x);
}
void mark(){ // marking each node with it's index in dfs array
int size = a.size();
// marks the index
for (int i = 0; i < size; i++) {
mape[a[i]] = i;
}
}
int main(){
int n = 7;
// add edges of a tree
addEdgetoGraph(1, 2);
addEdgetoGraph(1, 3);
addEdgetoGraph(2, 4);
addEdgetoGraph(2, 5);
addEdgetoGraph(4, 6);
addEdgetoGraph(4, 7);
// array to store the nodes present under of subtree
// of every node in a tree
int nodesunder[n + 1];
dfs(nodesunder, 1, 0); // generating our nodesunder array
mark(); // marking the indices in map
// Query 1
printDFS(2, nodesunder);
// Query 2
printDFS(4, nodesunder);
return 0;
} Đầu ra
The DFS of subtree 2: 2 4 6 7 5 The DFS of subtree 4: 4 6 7
Hiểu mã
Trong cách tiếp cận này, chúng tôi đang tính toán trước thứ tự của dfs và lưu trữ nó trong một vectơ bây giờ khi chúng tôi đã tính toán trước các dfs, chúng tôi cũng tính toán các nút hiện diện dưới mỗi cây con bắt đầu từ mỗi nút và sau đó chúng tôi chỉ cần duyệt qua chỉ số bắt đầu của nút sau đó cho tất cả số lượng nút hiện diện bên trong cây con của nó.
Kết luận
Trong hướng dẫn này, chúng tôi giải quyết một vấn đề để giải quyết các Truy vấn cho DFS của một cây con trong một cây. Chúng tôi cũng đã học chương trình C ++ cho vấn đề này và cách tiếp cận hoàn chỉnh (Bình thường) mà chúng tôi đã giải quyết vấn đề này.
Chúng ta có thể viết chương trình tương tự bằng các ngôn ngữ khác như C, java, python và các ngôn ngữ khác. Hy vọng bạn thấy bài viết này hữu ích.
