Trong bài toán này, chúng ta được đưa ra một cây nhị phân. Nhiệm vụ của chúng tôi là in truyền qua thứ tự sau của cây nhị phân mà không sử dụng đệ quy và không có ngăn xếp .
Cây nhị phân là một loại cây đặc biệt trong đó mỗi nút có thể có tối đa 2 nút con.
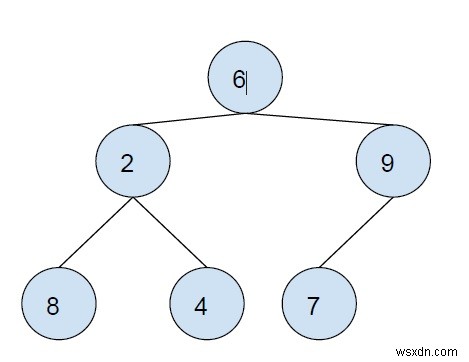
Truyền tải đơn hàng sau là một kỹ thuật duyệt cây, trong đó cây con bên trái đầu tiên được duyệt qua cây con bên phải và gốc được duyệt qua ở cuối.
đường đi ngang của cây trên - 8 4 2 7 9 6
Để đi qua cây mà không sử dụng đệ quy và ngăn xếp. Chúng tôi sẽ dựa trên kỹ thuật tìm kiếm theo chiều sâu và dữ liệu sẽ được lưu trữ trong bảng băm .
Ví dụ
Chương trình cho thấy việc triển khai giải pháp này,
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
void postOrderTraversal(struct Node* head) {
struct Node* temp = head;
unordered_set<Node*> visited;
while (temp && visited.find(temp) == visited.end()) {
if (temp->left &&
visited.find(temp->left) == visited.end())
temp = temp->left;
else if (temp->right &&
visited.find(temp->right) == visited.end())
temp = temp->right;
else {
cout<<temp->data<<"\t";
visited.insert(temp);
temp = head;
}
}
}
struct Node* insertNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main(){
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
} Đầu ra
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
Giải pháp tương tự có thể được cập nhật và việc sử dụng bảng băm có thể được loại bỏ. Vì công việc của nó là lưu trữ các nút đã truy cập. Chúng tôi sẽ thêm một cờ đã truy cập vào mỗi nút của chính nó là cây để giảm tải cho hệ thống, điều này sẽ làm cho thuật toán của chúng tôi tốt hơn.
Một giải pháp hiệu quả hơn là sử dụng một bản đồ không có thứ tự, điều này sẽ giảm chi phí theo dõi ngược lại cho người đứng đầu.
Ví dụ
Chương trình hiển thị việc thực hiện
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
bool visited;
};
void postOrderTraversal(Node* root) {
Node* n = root;
unordered_map<Node*, Node*> postorder;
postorder.insert(pair<Node*, Node*>(root, nullptr));
while (n) {
if (n->left && postorder.find(n->left) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->left, n));
n = n->left;
}
else if (n->right && postorder.find(n->right) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->right, n));
n = n->right;
}
else {
cout<<n->data<<"\t";
n = (postorder.find(n))->second;
}
}
}
struct Node* insertNode(int data) {
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
node->visited = false;
return (node);
}
int main() {
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
} Đầu ra
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
