Tích tối đa của hai đường dẫn không giao nhau trong một cây trong C ++

Trong bài toán này, chúng ta được cung cấp một cây được kết nối vô hướng T với n nút. Nhiệm vụ của chúng ta là tạo một chương trình để tìm tích số tối đa của hai đường dẫn không giao nhau trong một cây trong C ++.

Mô tả sự cố - Để tìm tích tối đa của hai đường đi không giao nhau trong một cây. Chúng tôi sẽ tìm tất cả các con đường không thú vị và sau đó tìm sản phẩm của độ dài của chúng.

Hãy lấy một ví dụ để hiểu vấn đề,

Đầu vào

Biểu đồ -

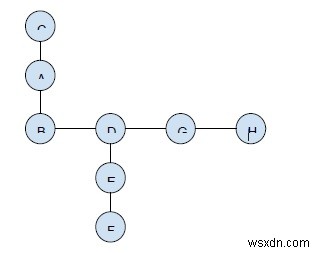
Đầu ra

8

Giải thích

Các đường dẫn không giao nhau được coi là C-A-B và F-E-D-G-H .

Độ dài là 2 và 4. Sản phẩm =8.

Phương pháp tiếp cận giải pháp

Giải pháp cho vấn đề này là duyệt cây bằng cách sử dụng DFS. Và tìm các đường dẫn sẽ là duy nhất nếu chúng ta loại bỏ cạnh kết nối. Và giới hạn trên con đường và tìm chiều dài của nó. Sau đó, chúng tôi sẽ ghép nối các đường dẫn và tìm sản phẩm có độ dài của chúng. Cả hai được xem xét theo cách mà sản phẩm của họ trở nên tối đa.

Chương trình triển khai giải pháp của chúng tôi,

Ví dụ

#include <bits/stdc++.h>
using namespace std;
int TreeTraverse(vector<int> graph[], int& currPathMax, int val1, int val2){
   int max1 = 0, max2 = 0, maxVal = 0;
   for (int i = 0; i < graph[val1].size(); i++) {
      if (graph[val1][i] == val2)
         continue;
         maxVal = max(maxVal, TreeTraverse(graph, currPathMax,
      graph[val1][i], val1));
      if (currPathMax > max1) {
         max2 = max1;
         max1 = currPathMax;
      }
      else
         max2 = max(max2, currPathMax);
   }
   maxVal = max(maxVal, max1 + max2);
   currPathMax = max1 + 1;
   return maxVal;
}
int FindMaxProductPath(vector<int> graph[], int Size) {
   int maxProd = -10;
   int pathA, pathB;
   int currPathMax, prod;
   for (int i = 0; i < Size; i++) {
      for (int j = 0; j < graph[i].size(); j++){
         currPathMax = 0;
         pathA = TreeTraverse(graph, currPathMax, graph[i][j],i);
         currPathMax = 0;
         pathB = TreeTraverse(graph, currPathMax, i,graph[i][j]);
         prod = (pathA * pathB);
         maxProd = max(maxProd, prod);
      }
   }
   return maxProd;
}
void insertEdge(vector<int> graph[], int val1, int val2){
   graph[val1].push_back(val2);
   graph[val2].push_back(val1);
}
int main(){
   int Size = 8;
   vector<int> graph[Size + 2];
   insertEdge(graph, 1, 2);
   insertEdge(graph, 2, 4);
   insertEdge(graph, 3, 1);
   insertEdge(graph, 5, 4);
   insertEdge(graph, 7, 8);
   insertEdge(graph, 8, 4);
   insertEdge(graph, 5, 6);
   cout<<"Maximum product of two non-intersecting paths of tree is "<<FindMaxProductPath(graph, Size)<<"\n";
   return 0;
}

Đầu ra

Maximum product of two non-intersecting paths of tree is 8