Đường kính cây trong C ++

Giả sử chúng ta có một cây vô hướng; chúng ta phải tìm đường kính của nó - số cạnh của con đường dài nhất trong cây đó là đường kính của cây đó. Ở đây cây được đưa ra dưới dạng danh sách cạnh trong đó các cạnh [i] =[u, v] là cạnh hai chiều giữa các nút u và v. Mỗi nút có các nhãn trong tập {0, 1, ..., edge.length}. Vì vậy, nếu biểu đồ giống như -

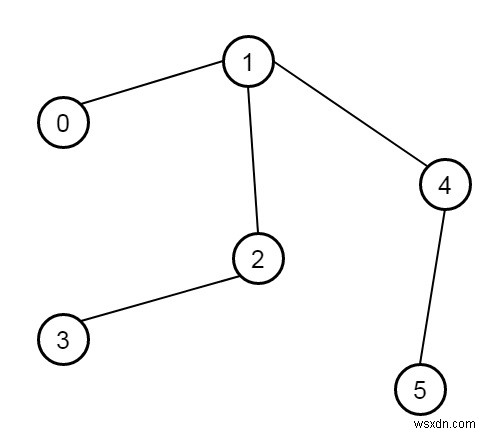
Đầu ra sẽ là 4.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

Xác định một bản đồ l
xác định một phương thức được gọi là dfs (). điều này sẽ nhận v, một mảng được gọi là đã thăm, đồ thị và c. Nó sẽ hoạt động như sau -
đã thăm [v]:=true, đặt ans:=0
cho tôi trong phạm vi từ 0 đến kích thước của biểu đồ [v]
- nếu truy cập [graph [v, i]] là false, thì
  - ans:=max of ans, dfs (graph [v, i], visit, graph, c + 1)
if c> best, then best:=c và node:=v
set đã truy cập [v]:=false
trả về giá trị tối đa của c và ans
Trong phương thức chính, nó sẽ sử dụng danh sách cạnh e
n:=kích thước của e, tạo một mảng được gọi là đồ thị có kích thước n + 1
cho tôi trong phạm vi từ 0 đến n - 1
- chèn e [i, 1] vào biểu đồ [e [i, 0]] và chèn e [i, 0] vào biểu đồ [e [i, 1]]
tạo hai mảng đã thăm và mảng đã thăm 2 có kích thước n + 1, đặt tốt nhất:=0 và nút:=0
gọi dfs (0, đã truy cập, biểu đồ)
trả về dfs (nút, lượt truy cập2, đồ thị)

Ví dụ (C ++)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
class Solution {
public:
   map <int ,int > l;
   int best;
   int node;
   int dfs(int v, bool* visited, vector <int> graph[], int c = 0){
      visited[v] = true;
      int ans = 0;
      for(int i = 0; i < graph[v].size(); i++){
         if(!visited[graph[v][i]])ans = max(ans,dfs(graph[v][i], visited, graph, c+1));
      }
      if(c > best){
         best = c;
         node = v ;
      }
      visited[v] = false;
      return max(c,ans);
   }
   int treeDiameter(vector<vector<int>>& e) {
      int n = e.size();
      vector <int> graph[n+1];
      for(int i = 0; i < n; i++){
         graph[e[i][0]].pb(e[i][1]);
         graph[e[i][1]].pb(e[i][0]);
      }
      bool* visited = new bool[n+1]();
      best = 0;
      node = 0;
      dfs(0, visited, graph);
      bool* visited2 = new bool[n+1]();
      return dfs(node, visited2, graph);
   }
};
main(){
   vector<vector<int>> v = {{0,1},{1,2},{2,3},{1,4},{4,5}};
   Solution ob;
   cout <<ob.treeDiameter(v);
}

Đầu vào

[[0,1],[1,2],[2,3],[1,4],[4,5]]