Giả sử có n thành phố khác nhau được đánh số từ 0 đến n-1 và cũng có n-1 con đường sao cho chỉ có một con đường để đi giữa hai thành phố khác nhau. Giả sử Bộ Giao thông vận tải quyết định định hướng các con đường theo một hướng vì chúng quá hẹp.
Ở đây, các con đường được biểu thị bằng các kết nối trong đó các kết nối [i] =[a, b] biểu thị một con đường từ thành phố a đến b.
Nếu có một sự kiện lớn ở thủ đô (thành phố được đánh số là 0), và nhiều người muốn đến thành phố này du lịch. Chúng ta phải thực hiện một số nhiệm vụ định hướng lại trên một số con đường để mỗi thành phố có thể đến thăm thành phố 0. Chúng ta phải tìm số cạnh tối thiểu đã thay đổi.
Vì vậy, nếu đầu vào là 6, các kết nối =[[0,1], [1,3], [2,3], [4,0], [4,5]],
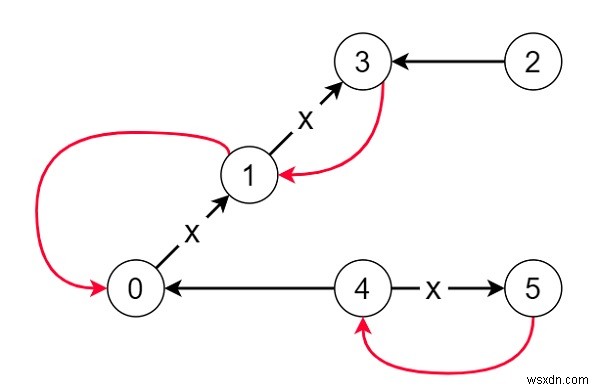
thì đầu ra sẽ là 3, vì chúng ta phải thay đổi hướng của các cạnh được hiển thị bằng màu đỏ để mỗi nút có thể đạt đến thủ đô.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Xác định hai mảng danh sách graph1, graph2 có kích thước N =5 * 10 ^ 4 + 5
-
Từ phương thức chính, thực hiện như sau -
-
Xác định một bản đồ trong
-
đối với mỗi phần tử nó trong e, thực hiện
-
chèn nó [1] vào cuối graph1 [it [0]]
-
chèn nó [0] vào cuối graph2 [it [1]]
-
-
Xác định một phân vùng có kích thước n và điền vào nó với N + 10
-
ret:=0, trong [0]:=0, dist [0]:=0
-
Xác định một hàng đợi q
-
chèn 0 vào q
-
Xác định một tập hợp đã truy cập
-
chèn 0 vào đã truy cập
-
while (không phải q trống), do -
-
node:=phần tử đầu tiên của q
-
xóa phần tử khỏi q
-
ret:=ret + dist [node]
-
đối với mỗi phần tử nó trong graph2 [node], thực hiện
-
nếu nó không được truy cập và dist [it]> 0, thì -
-
dist [it]:=0
-
chèn nó vào q
-
chèn nó vào đã thăm
-
-
-
đối với mỗi phần tử nó trong graph1 [node], thực hiện
-
nếu nó không được truy cập và dist [it]> 1, thì -
-
dist [it]:=1
-
chèn nó vào q
-
chèn nó vào đã thăm
-
-
-
-
trả lại ret
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5;
class Solution {
public:
vector<int> graph1[N];
vector<int> graph2[N];
int minReorder(int n, vector<vector<int> >& e){
map<int, int> in;
for (auto& it : e) {
graph1[it[0]].push_back(it[1]);
graph2[it[1]].push_back(it[0]);
}
vector<int> dist(n, N + 10);
int ret = 0;
in[0] = 0;
dist[0] = 0;
queue<int> q;
q.push(0);
set<int> visited;
visited.insert(0);
while (!q.empty()) {
int node = q.front();
q.pop();
ret += dist[node];
for (auto& it : graph2[node]) {
if (!visited.count(it) && dist[it] > 0) {
dist[it] = 0;
q.push(it);
visited.insert(it);
}
}
for (auto& it : graph1[node]) {
if (!visited.count(it) && dist[it] > 1) {
dist[it] = 1;
q.push(it);
visited.insert(it);
}
}
}
return ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1},{1,3},{2,3},{4,0},{4,5}};
cout << (ob.minReorder(6,v));
} Đầu vào
6,{{0,1},{1,3},{2,3},{4,0},{4,5}} Đầu ra
3
