Trong bài toán này, chúng ta được cung cấp một cây nhị phân BT. Nhiệm vụ của chúng ta là tạo một chương trình để tìm Tổng cây con tối đa trong Cây nhị phân sao cho cây con cũng là một BST.
Cây nhị phân có một điều kiện đặc biệt là mỗi nút có thể có tối đa hai nút con.
Cây tìm kiếm nhị phân là một cây trong đó tất cả các nút tuân theo các thuộc tính được đề cập dưới đây
-
Giá trị của khóa của cây con bên trái nhỏ hơn giá trị của khóa của nút cha (gốc) của nó.
-
Giá trị của khóa của cây con bên phải lớn hơn hoặc bằng giá trị của khóa của nút cha (gốc) của nó.
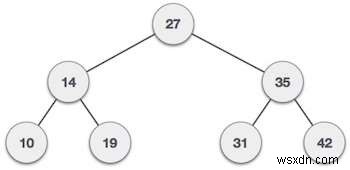
Hãy lấy một ví dụ để hiểu vấn đề,
Đầu vào
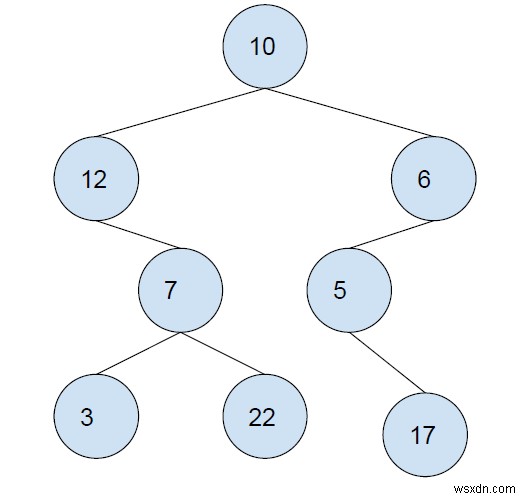
Đầu ra
32
Giải thích
Ở đây, chúng ta có hai cây con là BST. Tổng của chúng là,
7 + 3 + 22 = 32 6 + 5 + 17 = 28 Maximum = 32.
Phương pháp tiếp cận giải pháp
Một giải pháp đơn giản cho vấn đề là duyệt qua cấu trúc dữ liệu dạng cây và sau đó kiểm tra tại mỗi nút xem các nút con của nó có thể tạo thành cây Tìm kiếm nhị phân hay không. Nếu chúng tôi tìm thấy tổng của tất cả các nút đóng góp vào BST và sau đó quay trở lại mức tối đa của tất cả các nút đã tìm được của BSTSum.
Ví dụ
Chương trình minh họa hoạt động của giải pháp của chúng tôi,
#include <bits/stdc++.h>
using namespace std;
int findMax(int a, int b){
if(a > b)
return a;
return b;
}
int findMin(int a, int b){
if(a > b)
return b;
return a;
}
struct Node {
struct Node* left;
struct Node* right;
int data;
Node(int data){
this−>data = data;
this−>left = NULL;
this−>right = NULL;
}
};
struct treeVal{
int maxVal;
int minVal;
bool isBST;
int sum;
int currMax;
};
treeVal CalcBSTSumTill(struct Node* root, int& maxsum){
if (root == NULL)
return { −10000, 10000, true, 0, 0 };
if (root−>left == NULL && root−>right == NULL) {
maxsum = findMax(maxsum, root−>data);
return { root−>data, root−>data, true, root−>data, maxsum };
}
treeVal LeftSTree = CalcBSTSumTill(root−>left, maxsum);
treeVal RightSTree = CalcBSTSumTill(root−>right, maxsum);
treeVal currTRee;
if (LeftSTree.isBST && RightSTree.isBST && LeftSTree.maxVal <
root−>data && RightSTree.minVal > root−>data) {
currTRee.maxVal = findMax(root−>data,
findMax(LeftSTree.maxVal, RightSTree.maxVal));
currTRee.minVal = findMin(root−>data,
findMin(LeftSTree.minVal, RightSTree.minVal));
maxsum = findMax(maxsum, RightSTree.sum + root−>data +
LeftSTree.sum);
currTRee.sum = RightSTree.sum + root−>data +
LeftSTree.sum;
currTRee.currMax = maxsum;
currTRee.isBST = true;
return currTRee;
}
currTRee.isBST = false;
currTRee.currMax = maxsum;
currTRee.sum = RightSTree.sum + root−>data + LeftSTree.sum;
return currTRee;
}
int CalcMaxSumBST(struct Node* root){
int maxsum = −10000;
return CalcBSTSumTill(root, maxsum).currMax;
}
int main(){
struct Node* root = new Node(10);
root−>left = new Node(12);
root−>left−>right = new Node(7);
root−>left−>right−>left = new Node(3);
root−>left−>right−>right = new Node(22);
root−>right = new Node(6);
root−>right−>left = new Node(5);
root−>right−>left−>right = new Node(17);
cout<<"The maximum sub−tree sum in a Binary Tree such that the
sub−tree is also a BST is "<<CalcMaxSumBST(root);
return 0;
} Đầu ra
The maximum sub−tree sum in a Binary Tree such that the sub−tree is also a BST is 32
