Trong bài toán này, chúng ta được cung cấp một Cây nhị phân với mỗi nút có một giá trị. Nhiệm vụ của chúng ta là tạo một chương trình để tìm Tổng số nút tối đa trong Binarytree sao cho không có hai nút nào liền kề sử dụng Lập trình động.
Mô tả sự cố - Chúng tôi sẽ chọn các tập con của cây nhị phân để làm cho tổng lớn nhất theo cách mà các nút không được kết nối trực tiếp.
Hãy lấy một ví dụ để hiểu vấn đề,
Đầu vào
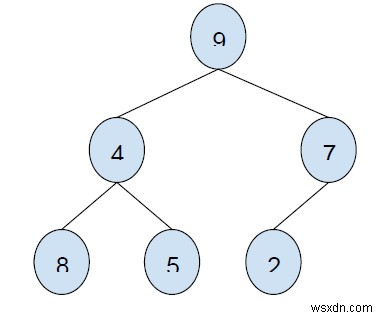
Đầu ra
24
Giải thích
Elements to be taken under consideration are: 8 + 5 + 9 + 2 = 24
Phương pháp tiếp cận giải pháp
Một giải pháp cho vấn đề là sử dụng một bản đồ và tìm tổng các nút mà chúng tạo thành maxSum. Cả hai nút và nút con của chúng không được
xét cho tổng theo điều kiện đã cho. Vì vậy, chúng ta cần kiểm tra thực tế là trước khi xem xét một nút, chúng ta cần kiểm tra xem cây con của nó có một số phần tử tạo thành tổng lớn hơn hay không.
Tìm tổng của cùng một cây con cha-con nhiều lần cho mỗi nút sẽ làm tăng chi phí tính toán và để giải quyết vấn đề đó, chúng tôi sẽ sử dụng tính năng ghi nhớ và lưu trữ maxSum cho đến nút trong một bản đồ có thể được sử dụng sau này.
Ví dụ
Chương trình minh họa hoạt động của giải pháp của chúng tôi,
#include <bits/stdc++.h>
using namespace std;
struct node{
int data;
struct node *left, *right;
};
struct node* newNode(int data){
struct node *temp = new struct node;
temp−>data = data;
temp−>left = temp−>right = NULL;
return temp;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum);
int sumSubTreeNodes(node* node, map<struct node*, int>& nodeSum){
int maxSum = 0;
if (node−>left)
maxSum += findMaxSumBT(node−>left−>left, nodeSum) +
findMaxSumBT(node−>left−>right, nodeSum);
if (node−>right)
maxSum += findMaxSumBT(node−>right−>left, nodeSum) +
findMaxSumBT(node−>right−>right, nodeSum);
return maxSum;
}
int findMaxSumBT(node* node, map<struct node*, int>& nodeSum){
if (node == NULL)
return 0;
if (nodeSum.find(node) != nodeSum.end())
return nodeSum[node];
int sumInclCurr = node−>data + sumSubTreeNodes(node, nodeSum);
int sumExclCurr = findMaxSumBT(node−>left, nodeSum) +
findMaxSumBT(node−>right, nodeSum);
nodeSum[node] = max(sumInclCurr, sumExclCurr);
return nodeSum[node];
}
int main(){
node* root = newNode(9);
root−>left = newNode(4);
root−>right = newNode(7);
root−>left−>left = newNode(8);
root−>left−>right = newNode(5);
root−>right−>left = newNode(2);
map<struct node*, int> nodeSum;
cout<<"Maximum sum of nodes in Binary tree such that no two are
adjacent using Dynamic Programming is "<<findMaxSumBT(root,
nodeSum);
return 0;
} Đầu ra
Maximum sum of nodes in Binary tree such that no two are adjacent using Dynamic Programming is 24
